Christopher Higginbotham
CSCI 322
19 October 1999
______________________________________________________________________________________________________
Lab #2
Objective:
The purpose of this lab was to look into a particular area of artificial intelligence programming. Once an area of interest is found we are supposed to find a program already programmed in LISP and either add more functionality to the program or perform a detailed analysis of the program.
Introduction:
The particular area of artificial intelligence that I was interested in was game development artificial intelligence. I wanted to learn about how computer games uses artificial intelligence to perform decision-making. One of the first web sites that I visited was http://www.gameai.com/ai.html. This link provided some good links to a lot of theory on how decision making is done in games. In particular I went to the website http://www.coba.drexel.edu/economics/mccain/game/game.html and read about some basic game theory. "Game theory is a distinct and interdisciplinary approach to the study of human behavior."1 This is because a game must perform the same logical decisions that a human has to make in order to be competitive.
There are many different strategies used within game theory. One of these theories is the zero-sum theory. "If we add up the wins and losses in a game, treating losses as negatives, and we find that the sum is zero for each set of strategies chosen, then the game is a "zero-sum game. "In less formal terms, a zero-sum game is a game in which one player's winnings equal the other player's losses. Do notice that the definition requires a zero sum for every set of strategies. If there is even one strategy set for which the sum differs from zero, then the game is not zero sum."2 This theory is used to explain that minimizing your losses would automatically maximize your gain.
Another topic that I did some looking into was finding an optimal pathfinder for vehicles in real-world digital terrain maps. I read the thesis paper at http://www.student.nada.kth.se/~f93-maj/pathfinder/preface.html. This paper described a master students thesis solution to this problem which involved factoring in geographical information in order to find the shortest possible path from one place to another.
Finally through all of this reading and research I came across Conway’s Game of Life. I had heard about this game and did some research on how this game worked. I found many sites that had Java programs running on there site and free downloads for Microsoft versions of this game. I realized that Conway’s Game of Life was not really a game but a rule based simulation. I was able to tinker around with the Java programs to get a better understanding on what was actually involved with this program. I also found a version of Conway’s Game of Life implemented in LISP that I could do this lab report on.
Discovery & Approach:
Conway’s Game of Life is a rule-based simulation. The basic setup for the game is a grid area that contains either a Boolean value 0 or 1 in each cell space. A zero means that there is nothing in the space and one means that the space is occupied by a cell. The rules for the simulation are the following:
Rules for Conway’s Game of Life:
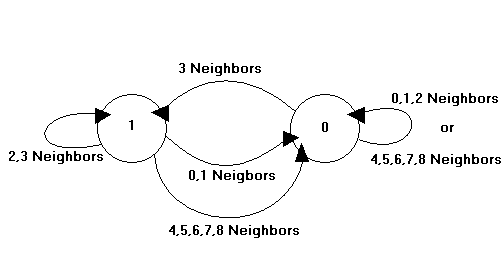
Finite State Machine for Rules of Conway’s Game of Life:

Methods & Structures:
This section gives a list of all the methods and structures used in the implementation I have on Conway’s Game of Life. It also provides a pseudo code representation of what each method performs.
Structure: World
Elements: size – size of element arrays
current – current state of a bit
numdots – number of living cells
next – next state of a bit
xmin – minimum cell position along the x axis.
xmax – maximum cell position along the x axis.
ymin – minimum cell position along the y axis.
ymax – maximum cell position along y axes.
print() – outputs the string "#<WORLD: n>" where n is numdots.
Method: Life()
Purpose: The purpose of this method is to read in the data set, initialize the data structure world with the data set information, and start the game of life.
Inputs: source - a list of lists which contain 0 or 1 indicating if a space contains a cell.
Pseudo Code:
Assigns size to the first list element in source.
Creates an instance of world named life with the following parameters.
world.size = size
world.curent[size].element-type to bit value
world.current[size].initial-contents to source
world.next[size].element-type to bit value
world.next[size].initial-contents to 0
world.numdots = 0
Start For loop using i as incremental and size as max
Start For loop using j as incremental and size as max
Increment world.numdots
if (i > world.xmin)
world.xmin = i
if (i < world.xmax)
world.xmax = i
if (j > world.ymin)
world.ymin = j
if (j < world.ymax)
world.ymax = j
Call method Propogate with parameters life and 0.
Method: Propogate()
Purpose: The purpose of this method is to start a main loop that will cause keep calculating generations of cells either infinitely or until the number of cells equals 0.
Inputs: world – data structure containing all the source information that was calculated in life method.
cycles – number of cycles that this program has propagated.
Pseudo Code:
Call method Print-World with parameters world and cycles.
Start a do loop that will loop while world.numdots != 0.
Call method Next-Cycle with parameter world.
Increment cycles variable
Call method method Print-World with parameters world and cycles.
Method: Print-World()
Purpose: The purpose of this method is to output the source grid to the screen with information about the number of cells on the plot and the current propagation of this output.
Inputs: world – data structure containing all the source information.
generations – number of cycles that this program has propagated.
Pseudo Code:
Set lim = world.size
Set current = world.current
Start a For loop from y = 0 to y < lim incrementing y++
Start a For loop from x = 0 to x < lim incrementing x++
if (current = 0)
Output a space
else
Output an asterik
Output String "x Generation, y Organisms" where x = generations and y = world.numdots
Method: Next-Cycle()
Purpose: The purpose of this method is to loop through all the cells in the grid and call Set-Next on them.
Inputs: world – data structure containing all the source information.
Pseudo Code:
Set lim = world.size
Set current = world.current
Set next = world.next
Set xlb = max(1, world.xmin – 1)
Set xub = min(lim – 1, world.xmax + 1)
Set ylb = max(1, world.ymin – 1)
Set yub = min(lim – 2, world.ymax + 1)
Start a For loop from i = 0 to y < ((xub-xlb)+1 incrementing i++
Start a For loop from j = 0 to j < ((yub-ylb)+1 incrementing j++
Call method SetNext with parameters world, (i+xlb),(j+ylb)
Start a For loop from y = 0 to y < lim incrementing y++
Start a For loop from x = 0 to x < lim incrementing x++
Set current bit at (x,y) to next bit (x,y)
Method: Setnext()
Purpose: The purpose of this method is to perform the logic rules on the current cell space based on the finite state machine above.
Inputs: world – data structure containing all the source information.
Pseudo Code:
Set current = world.current
Set next = world.next
Set neighbors = method CountNeighbors with parameters current, i, and j.
if (current bit = 0)
if (neighbors != 3)
Set next bit (i,j) to 0
else
Set next bit(i,j) to 1
increment world.numdots
else
if (neighbors = 2 || neighbors = 3)
Set next bit (i,j) to 1
else
Set next bit (i,j) to 0
decrement world.numdots
if (next bit (i,j) != 0
if (i > world.xmin)
world.xmin = i
if (i < world.xmax)
world.xmax = i
if (j > world.ymin)
world.ymin = j
if (j < world.ymax)
world.ymax = j
Conclusion:
A certain pattern that I really liked messing around with was the following infinitely stable pattern:

I found that if I added one pixel to it like so:

I could get the following pattern to occur, which are four instances of the original stable pattern:

If I added the same pixel as I did in the second snapshot, it completely wiped out all the cells:

What I found in my results is that two things would happen after running this program. Eventually all the cells would die after so many propagation’s, or a group of cells would form a certain pattern that would oscillate infinitely. This was a very fun program to mess around with because I found out that after setting up a certain pattern I could either wipe out the cells or cause some interesting oscillation patterns to occur. This program definitely had some basic rule-based artificial intelligence. I was hoping that I could find a game programmed in LISP with more interesting artificial intelligence then this game had.
Source Code:
Website:
http://www.cs.cmu.edu/afs/cs/project/ai-repository/ai/lang/lisp/code/fun/
;;; ****************************************************************
;;; Conway's Game of Life ******************************************
;;; ****************************************************************
;;; Don't know where/when got this. --mk
(defstruct (world (:print-function
(lambda (s d o)
(declare (ignore d))
(format s "#<WORLD: ~D>" (world-numdots world)))))
size
current
numdots
next
(xmin 1000000) ; Initialize the region to ridiculous numbers.
(xmax -1)
(ymin 1000000)
(ymax -1))
(defun setnext (world i j)
(let* ((current (world-current world))
(next (world-next world))
(neighbors (count-neighbors current i j)))
;; set the next bit pattern
(if (zerop (bit current i j))
(cond ((not (= neighbors 3))
;; current = 0, surrounding cells != 3
(setf (bit next i j) 0))
(t (setf (bit next i j) 1)
;; current = 0, surrounding cells = 3
(incf (world-numdots world))))
(cond ((or (= neighbors 2)
(= neighbors 3))
;; current = 1, surrounding cells = 2,3
(setf (bit next i j) 1))
(t (setf (bit next i j) 0)
(decf (world-numdots world)))))
;; reset the bounds, if necessary
(unless (zerop (bit next i j))
(when (< i (world-xmin world)) (setf (world-xmin world) i))
(when (> i (world-xmax world)) (setf (world-xmax world) i))
(when (< j (world-ymin world)) (setf (world-ymin world) j))
(when (> j (world-ymax world)) (setf (world-ymax world) j)))))
(defun count-neighbors (array i j)
(+ (bit array (1- i) (1- j))
(bit array i (1- j))
(bit array (1+ i) (1- j))
(bit array (1- i) j)
(bit array (1+ i) j)
(bit array (1- i) (1+ j))
(bit array i (1+ j))
(bit array (1+ i) (1+ j))))
(defun next-cycle (world)
(let* ((lim (world-size world))
(current (world-current world))
(next (world-next world))
(xlb (max 1 (1- (world-xmin world))))
(xub (min (- lim 2) (1+ (world-xmax world))))
(ylb (max 1 (1- (world-ymin world))))
(yub (min (- lim 2) (1+ (world-ymax world)))))
(dotimes (i (1+ (- xub xlb)))
(dotimes (j (1+ (- yub ylb)))
(setnext world (+ i xlb) (+ j ylb))))
(dotimes (y lim)
(dotimes (x lim)
(setf (bit current x y) (bit next x y))))))
(defun print-world (world generations)
(let ((lim (world-size world))
(current (world-current world)))
(dotimes (y lim)
(dotimes (x lim)
(if (zerop (bit current y x))
(princ " ")
(princ "*")))
(terpri))
(format t "~&~d Generations, ~d Organisms."
generations (world-numdots world))))
(defun propagate (world cycles)
(print-world world cycles)
(do ()
((zerop (world-numdots world))
(format t "~2&POPULATION 0 ... ~d generations" cycles))
(next-cycle world)
(incf cycles)
(print-world world cycles)))
(defun life (source)
(let* ((size (length (car source)))
(life (make-world
:size size
:current (make-array (list size size) :element-type 'bit
:initial-contents source)
:next (make-array (list size size) :element-type 'bit
:initial-element 0)
:numdots 0)))
(dotimes (i size)
(dotimes (j size)
(unless (zerop (bit (world-current life) i j))
(incf (world-numdots life))
(when (< i (world-xmin life)) (setf (world-xmin life) i))
(when (> i (world-xmax life)) (setf (world-xmax life) i))
(when (< j (world-ymin life)) (setf (world-ymin life) j))
(when (> j (world-ymax life)) (setf (world-ymax life) j)))))
(propagate life 0)))
#|
;;; Example:
(setq test
'((0 0 0 0 0 0 0 0)
(0 0 0 1 1 0 1 0)
(0 0 1 0 1 0 1 0)
(0 0 1 1 1 0 0 0)
(0 1 0 0 1 1 1 0)
(0 1 1 1 0 0 0 0)
(0 0 0 1 1 0 1 0)
(0 0 0 0 0 0 0 0)))
(life test)
|#
;;; *EOF*
Running Code:
Sample Test Data:
(setq test
'((0 0 0 0 0 0 0 0)
(0 0 0 1 1 0 1 0)
(0 0 1 0 1 0 1 0)
(0 0 1 1 1 0 0 0)
(0 1 0 0 1 1 1 0)
(0 1 1 1 0 0 0 0)
(0 0 0 1 1 0 1 0)
(0 0 0 0 0 0 0 0)))
After adding a test set like the example from the source code.
Type the following: (life test)
Sources for Conway’s Game of Life:
http://www2.ecst.csuchico.edu/~binnur/javaLab2/Life.html
http://www.mindspring.com/~alanh/life/
http://users.hol.gr./~xpolakis/jhc/jhc_gol.html
http://www.bitstorm.org/gameoflife/
http://www.inmet.com/javadir/download/demo/LifeRect.html
References:
1,2 - http://www.coba.drexel.edu/economics/mccain/game/game.html
Other References: