Genetic Algorithms

Function optimization

\arg\max_\mathbf{x} f(\mathbf{x})

• \mathbf{x}: genome

• f: some “black box” function

Neuroevolution

\mathbf{w}: weights of a neural network

• Here we consider only networks with a fixed structure

f(\mathbf{w}): how well a network does at some task

• For example, classification or control

Now f is less opaque: we know something about how each element of \mathbf{w} relates to each other.

Enforced Subpopulations (ESP) [1]

Each neuron gets its own population

Different individuals are chosen at random to make an entire network

The fitness of an individual is the average of the fitnesses of all the networks it participated in

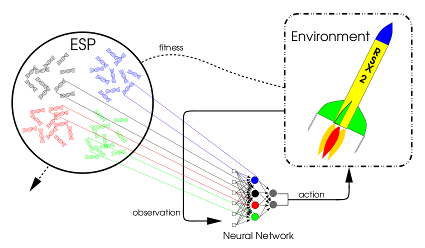
Enforced Subpopulations

Linkage

“Building blocks” in a genome are formed from related (linked) alleles

Respecting linkage during crossover preserves these building blocks

ESP building blocks: neurons

2D Pole Balancing [2]

2D pole balancing environment

Finless Rocket Guidance [3]

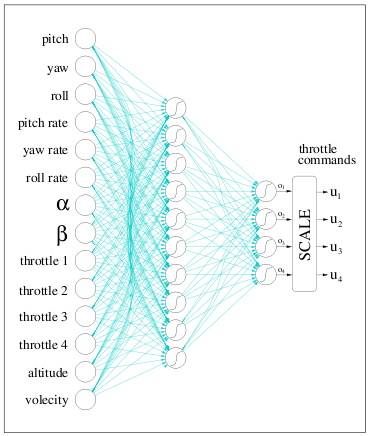
finless rocket guidance network

We Can Do Better!

• Linkage exists at levels higher than the neuron in both of these problems

• How to automatically protect building blocks without a priori knowledge?

• linkage-learning

Bibliography

[1] F. Gomez and R. Miikkulainen, “Incremental Evolution of Complex General Behavior,” Adaptive Behavior, vol. 5, 1997, pp. 317–342. 

[2] F. Gomez and R. Miikkulainen, “2-D pole balancing with recurrent evolutionary networks,” ICANN, 1998, p. 758–763.

[3] F. Gomez and R. Miikkulainen, “Active guidance for a finless rocket using neuroevolution,” GECCO, 2003, p. 2084–2095.