The Compact and Extended Compact GA
by J.D. Marble on February 1, 2010Overview
Not a computer display standard!
Compact Genetic Algorithm (CGA)
Extended Compact Genetic Algorithm (ECGA)
Compact Genetic Algorithm
Represents the population as a probability distribution (multiple, independent Bernoulli distributions)
Less memory used than GA
Less bandwidth used in master/slave parallel implementation
“Operationally equivalent to the order-one behavior of the simple GA with uniform crossover”
cGA Algorithm
- Initialize probability vector
p \leftarrow \langle 0.5, 0.5, \cdots, 0.5 \rangle
- Generate two individuals from the vector
a \leftarrow generate(p)
b \leftarrow generate(p)
- Let them compete
winner \leftarrow evaulate(a, b)
- Update the probability vector towards the better one
p \leftarrow p + (2 winner - 1)/n
- Repeat from step 2 until converged
Extended Compact Genetic Algorithm
Like cGA, represents the population as a probability distribution
“The choice of a good distribution is equivalent to linkage learning.”
“…simpler distributions are better than complex ones.” (Occam’s Razor)
Marginal Product Model (MPM)
- Example:
bits 0,3 p bit 1 p bit 2 p 00 0 .5 0 0 .5 0 0 .5 01 0 .0 1 0 .5 1 0 .5 10 0 .0 11 0 .5
ECGA Algorithm
Generate a random population
Undergo tournament selection
Model the population using a greedy MPM search
Generate a new population using the given model
Repeat until converged
ECGA Algorithm
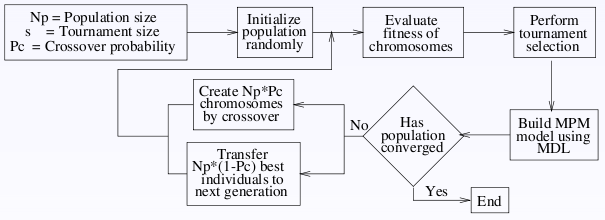
ECGA Algorithm Flowchart
Future work
Study existing implementations of real-coded ECGAs
Find modularity in the model
Apply to 2-D pole balancing and finless rocket guidance problems
???
Profit!
Bibliography
[1] G. Harik, “The compact genetic algorithm,” IEEE Transactions on Evolutionary Computation, vol. 9, 1999, pp. 38–297.
[2] G. Harik, “Linkage learning via probabilistic modeling in the ECGA,” Urbana, IL: University of Illinois at Urbana-Champaign, 1999.
[3] K. Sastry and D.E. Goldberg, “On Extended Compact Genetic Algorithm,” Urbana, IL: University of Illinois at Urbana-Champaign, 2000.
