Upper Division Problem F: What the Hail?
Upper Division G: Elo
Upper Division Problem H: Sum of Powers
Upper Division Problem I: Shortest Paths
Upper Division Problem J: Death to Gophers
Problem A: Horizontal Histogram
Write a program that accepts a set of digits (0 to 9) as input and prints a horizontal histogram representing the occurrences of each digit.Input:
First the number of tests, second one per line the numbers.
Sample Input
2
13
172967137579
Sample Output
0 1 * 2 3 * 4 5 6 7 8 9 0 1 ** 2 * 3 * 4 5 * 6 * 7 **** 8 9 **
Problem B: Rock, Paper, Scissors?
Rock, Paper, Scissors is a two player game, where each player simultaneously chooses one of the three items after counting to three.
The game typically lasts a pre-determined number of rounds. The player who wins the most rounds wins the game.
Given the number of rounds the players will compete, it is your job to determine which player wins
after those rounds have been played.
The rules for what item wins are as follows.
- Rock always beats Scissors (Rock crushes Scissors)
- Scissors always beat Paper (Scissors cuts Paper)
- Paper always beats rock (Paper covers Rock)
Input:
The first value in the input will be an integer t (0 < t < 1000) representing the number of test cases in the input. Following this, on a case by case basis, will be an integer n (0 < n < 100) specifying the number of rounds of Rock, Paper, Scissors played. Next will be n lines, each with either a capital R,P, or S, followed by a space, followed by a capital R,P, or S, followed by a newline. The first letter is player 1's choice; the second letter is paleyer 2's choice.
Output:
for each test case, report the name of the player (Player 1 or Player 2) that wins the game, followed by a newline. If the game ends up in a tie, print TIE.
Sample Input
3 2 R P S R 3 P p R S S R 1 P R
Sample Output
Player 2 TIE Player 1
Problem C: String Compression
Description
Consider the string AAAABCCCCCDDDD consisting of alphabetic characters only. This string is of length 14. Since the string consists of alphabetic characters only, duplicate characters can be removed and replaced with a duplication factor n. With this technique the string can be compressed and represented by 4AB5C4D. The compressed string is of length 7. Write a program which takes a string in compressed form and recreates the original uncompressed string.Input
The string will be of the format nA... where n, the duplication factor, is an integer between 2 and 99 and A is an uppercase alphabetic character. A string may contain single characters not prefixed with a duplication factor. If this were not the case, for instance, the string AABCDE would be compressed to 2A1B1C1D1E. To avoid this, single characters will not be prefixed with a duplication factor. The string AABCDE would be compressed to 2ABCDE.
The maximum length of an input string is 80 characters.
Output
The uncompressed string, 40 characters per line (it may be necessary to break an uncompressed string over multiple lines).
Example 1
Input
3A4B7D
Output
AAABBBBDDDDDDD
Example 2
Input
22D7AC18FGD
Output
DDDDDDDDDDDDDDDDDDDDDDAAAAAAACFFFFFFFFFF FFFFFFFFGD
Lower Divison Problem D: Rotating Words
Description
You are required to rotate a word a certain amount. For example, to rotate the word "Computer" by 1 results in "rCompute". Rotating it two more times gives you "terCompu".
Input:
The first line contains the number of tests cases.
Subsequent lines contain the word (which will not have more than 15 letters). And the number of characters to rotate n, which will be less than the length of the word. You must rotate the word n times.
Output:
Each rotated word, one per line
Sample Input
4 Computer 3 Program 1 eseWizChe 15 HelloWorld -3
Sample Output
terCompu mProgra WizCheese loWorldHel
Problem E: Bubble Gum, Bubble Gum
Alex and Karyn were at it again. The elementry school sisters were playing thier favorite game to decide who gets to play on the computer next.
The rules of the game are quite simple. Given p people (p > 0), one of the p people is chosen to pick a number n (n > p) representing the number of pieces of bubble gum desired. Once this value is chosen, the people are iterated through, one at a time, starting at 1, from "left" to "right", starting with the person who chose the number. Iterating is done in a circular fashion, meaning that once the person on the far right is reached, the next person in the iteration will be the person on the far left. Upon reaching n, the person chose, determine who wins the game.
INPUT:
The first value in the input will be an integer t (0 < t < 1000) representing the number of test cases in the input file. Following this, on a case by case basis, will be the list of names of the people (p), on a single line. Names will be no linger than 20 characters in length and all names are unique. There will be no more than 20 names. Each name is followed by a space, save for the last name, which is followed by a newline. The test case is concluded with the number of pieces of gum n(p < n < 1000), which is followed by a newline.
OUTPUT:
For each test case repost the name of the person who won the game, followed by a newline.
SAMPLE INPUT
3 Alex Karyn Maude Karyn 5 Alex Karyn Maude Alex 6 Alex Karyn Zach Becca Maude Zach 8
SAMPLE OUTPUT
Maude Maude Maude
Problem F: What the Hail?
Description:
There is an interesting series of integers known as hailstones. Hailstones are formed by being given a starting integer and generating the next integer based on the one that immediately precedes it in the series as follows: If the previous integer was even, the next integer in the series is half of it. If the previous integer was odd, the next integer is three times it plus one. Although the series goes up and down (like hailstones before they fall to rest on the ground), it eventually settles into a steady state of 4, 2, 1, 4, 2, 1, 4, 2, 1, For example, starting at 21, the hailstones series is: 21, 64, 32, 16, 8, 4, 2, 1, 4, 2, 1, For 21, the series required five steps before the steady state was reached.
Write a program that computes the number of steps necessary to reach the steady state in the hailstone series beginning at a given positive integer.
The input file will first contain the number of tests. The input file will contain a sequence of one or more positive integer values, one per line.
Sample Input:
2 21 10
Output:
5 steps were necessary for 21.4 steps were necessary for 10.
Additional notes:
You know that you have reached steady state when a 4 is reached in the series.
You may assume that all input values will be positive integers.
Problem G: ELO
Imagine a lab full of people, who play games every friday afternoon.
In order to help streamline the match making process, they want to develop a program that can help match players against one another.
A key aspect of this is a rating system, each player should have a rating which is updated after each game.
The Elo system, developed by Árpád Élo, is the classic game ranking system used in chess.
Each player has a ranking, and the system provides functions to estimate the expected score both players in a match. Victory -> 1, Loss -> 0.
If Player A has true strength RA and Player B has true strength RB, the expected score of Player A is
Similarly the expected score for Player B is
Note that EA + EB = 1.
When a player's actual score exceed his expected scores, the ELO system takes this as evidence that player's rating is too low, and needs to be adjusted upward. Similarly when a player's actual tournament scores fall short of his expected scores, that player's rating is adjusted downward. Élo's original suggestion, which is still widely used, was a simple linear adjustment proportional to the amount by which a player overperformed or underperformed his expected score. The maximum possible adjustment per game (sometimes called the K-value) was set at K = 16 for masters and K = 32 for weaker players in chess.
Supposing Player A was expected to score EA points but actually scored SA points. The formula for updating his rating is
Input:
The program will first read in the K-value to use and the number of players.
It will then read in, one per line player names and rankings.
Then the number of matches will follow, with one match per line, [player1] vs [player2] = [winningPlayer].
The program will then read in a list of matches, describing who played against who, and what the result was.
Your program should update each players rankings after each match, outputting each players ultimate rankings.
Output:
Your program should output each player's name + their new rating, one per line seperated by a single space.
Sample Input:
100
7
James 1240
Robert 1310
William 1050
Mary 1350
Patricia 930
Linda 1290
Elizabeth 1130
5
James vs Patricia = Patricia
Robert vs William = Robert
Elizabeth vs Linda = Elizabeth
Elizabeth vs Mary = Elizabeth
Mary vs James = Mary
Sample Output:
James 1122
Robert 1328
William 1032
Mary 1313
Patricia 1016
Linda 1218
Elizabeth 1272
Problem H: Sum of powers
A young schoolboy would like to calculate the sum
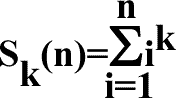
for some fixed natural k and different natural n. He observed that calculating ik for all i (1<=i<=n) and summing up results is a too slow way to do it, because the number of required arithmetical operations increases as n increases. Fortunately, there is another method which takes only a constant number of operations regardless of n. It is possible to show that the sum Sk(n) is equal to some polynomial of degree k+1 in the variable n with rational coefficients, i.e.,
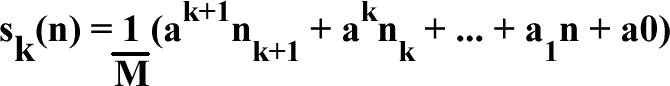
for some integer numbers M, ak+1, ak, ... , a1, a0.
We require that integer M be positive and as small as possible. Under this condition the entire set of such numbers (i.e. M, ak+1, ak, ... , a1, a0) will be unique for the given k. You have to write a program to find such set of coefficients to help the schoolboy make his calculations quicker.
Input
The input file contains a single integer k (1<=20).
Output
Write integer numbers M, ak+1, ak, ... , a1, a0 to the output file in the given order. Numbers should be separated by one or more spaces. Remember that you should write the answer with the smallest positive M possible.
Sample input
2
Output for the sample input
6 2 3 1 0
Problem I: Shortest Paths
Given a directed graph G=(V, E), and a source vertex v0ÎV, please write a program to output the lengths of the shortest paths between v0 and all other vertices in the graph G. We assume the edges in digraph G can have negative costs, provided that the sum of the costs around any cycle in the digraph is positiv. The vertices are labeled from 1 to n, if G has n vertices. The data fromats of the input and the output of this problem are arranged as follows.
Input
Your program must accept the following input
- A positive integer n, it stands for the total number vertices of G.
- A source vertex v0 (v0ÎV, i.e., it could be any vertex in G.)
- The cost matrix W of G. It is arranged by row-wise order as follows.
the first row of cost matrix W (enter)
the second row of cost matrix W (enter)
...
the last row of cost matrix W (enter)
Output
The lengths of the shortest paths from v0 to all other vertices vi, the format is (v0 -> vi) = ?
Notes:
- In the input, we arrange the input data W(vi, vj) = '-', if (vi, vj) is not an edge in G, vi¹vj, and W(vi, vj) = 0, if vi=vj.
Example:
Assume we have the following 5-vertex digraph G and its cost matrix W.

If we let v0 = 1, then yout input data must be
5 1 0 2 - - 10 - 0 3 - 7 - - 0 4 - - - - 0 5 - - 6 - 0
and the output would be
(1 -> 2) = 2
(1 -> 3) = 5
(1 -> 4) = 9
(1 -> 5) = 9
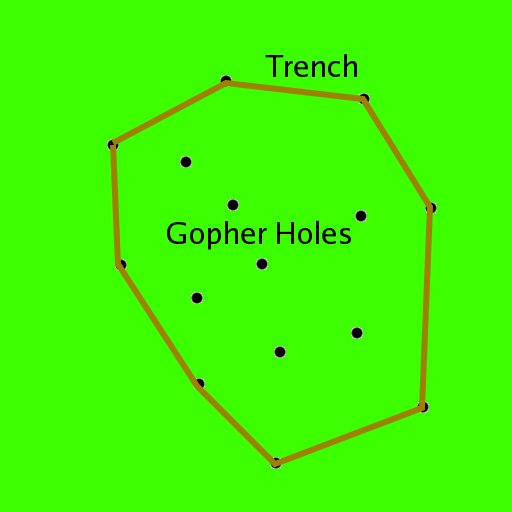
Problem J: Death to Gopher's
Carl Spackler hates gophers, and his latest plan to destroy them is too dig a 10 foot deep trench around their holes, and then fill the trench and cover the ground inside of it with concrete.
Then once they are trapped any variety of unspeakable chemical or biological weaponry can be used to destroy them.
An unlimited amount of concrete is available, but the trenching equipment is in short supply.
Your program will read in the locations of the gopher holes, and then determine and display the optimal trench encompassing them.
Hint: Shortest Trench = Convex Polygon
You can assume the points lie between 0,0 and 1024, 1024 and there is at most 1024 of them.


Input Description
Each problem is described by a set of points marking the locations of the gopher hole. Each line will contain a point, with problems being seperated by a a single empty line.xgraph
Hint: xgraph is an excellent program that provides a quick and dirty way to display the points, it should also work on your output (xgraph inputq outputq) If its not on your machine you can try grabbing a binary hereOutput
For each setup described in the input file output the sequence of points comprising the trench.
List the points comprising the trench path, each on a seperate line.
Use a single blank space between output files.
Sample Input
10 10 30 50 125 175 195 25 215 85 315 45 315 115
Sample Output
10 10 30 50 125 175 315 115 315 45 195 25 10 10