The goal of this assignment was to implement a GA to solve the symmetric TSP problem. In the symmetric TSP problem, the distance from city A to city B is the same as the distace from city B to city A. The fitness is given by the euclidean distances between cities in a tour.

I initially used the canonical GA to solve the symmetric TSP problem. On the canonical GA, I used PMX as the crossover operator as discussed by Goldberg in the book Genetic algorithms in search, optimization and machine learning. I also used the mutation operator discussed in the book, which consisted of swapping two random cities in a tour. The canonical GA uses roulette wheel selection, and no linear scaling was used.

The canonical GA performed very badly on the TSP problem. It was never able to converge to a good solution, and without the use of an elitist technique, even the inviduals with the highest performance could be lost. On the canonical GA I used a population size of 500 and ran the GA for 500 generations. Running it for more generations did not increase the performance of the GA. Furthermore, I used a probability of crossover of 0.95 and probability of mutation of 0.05. Below are graphs of the performance of the canonical GA on the eil51 and eil75 tours. The graphs show the GA performance over 30 runs. The graphs show a comparison of the first 10 runs of the GA, all 30 runs of the GA, and the average-maximum, average-minimum, and average-average fitnesses of individuals over all 30 runs.

eil51

eil76

Now I will show how a GA with elitism outperforms the canonical GA in the solving the TSP problem. I used the CIGAR for TSPs code found in the website of Dr. Sushil Loius at http://www.cse.unr.edu/~sushil/class/gas/code/cigar/cigartsp-1.1.tgz. I set up the CIGAR so that it runs as a GA, so it does not use the case injection. Here I again used a population size of 500, yet I only ran the GA for 200 generations, instead of 500 as in the canonical GA. I used crossover probability of 0.76 and a mutation rate of 0.1. The code uses CHC elitism, with a lamba value of 3. So each generation the population is tripled, then the individuals in this population are sorted, and the top 500 individuals are chosen. Thus, we never lose the highest fitness individuals and we make the GA concentrate on promising areas. Moreover, I used a scaling factor of 1.3.

The CIGAR code also used the same PMX crossover implementation as discussed by Goldberg in the same book. The mutation operator was also the same as in the canonical GA. Below are graphs of the performance of the CIGAR code on the same two tours, eil51 and eil76. The graphs show a comparison of the first 10 runs of the GA, all 30 runs of the GA, and the average-maximum, average-minimum, and average-average fitnesses of individuals over all 30 runs.

eil51
   Comparison of First 10 runs of the CIGAR
   
   Comparison of All 30 runs of the CIGAR
   
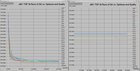
   Average-max, average-average, and average-min
   

eil76
   Comparison of First 10 runs of the CIGAR
   
   Comparison of All 30 runs of the CIGAR
   
   Average-max, average-average, and average-min