Recursion

Consider the following problem: Write a function that calculates the factorial of a number, where the factorial of an integer n, denoted n! is n! = n * (n - 1) * (n - 2) * ... * and 0! = 1. Another way of saying the same thing is to say that the factorial of 0 is 1 and n! = n * (n - 1)!. n! is not defined for negative numbers.

If we were to write a normal iterative function to calculate the factorial of a number, we would probably use a for loop and call the function from a program like the one below:

#include <stdio.h>
#include <assert.h>  /* needed for ussing the assert macro */

int fact(int);

int main(int argc, char * argv[])
{
  int n;
  assert(argc == 2); /* check number of arguments */

  n = atoi(argv[1]); /* get command line argument */
  printf("The factorial of %i is %i\n", n, fact(n)); /* invoke fact()*/
}

int fact(int input)
{
  int i, prod = 1;
	/* input! = input * input-1 * input-2 *... */
  for (i = input; i != 0; i--)
    {
      prod *= i; /* calculate running product */
    }
  return prod;
}

This works quite well, as you can find out by compiling and running the code, however, it looks nothing like our definition of factorial. We can write a recursive version of the fact() function that looks much more like our original definition of n! where 0! = 1 and n! = n * (n-1)!. Recursive means the function invokes itself, presumably with different arguments. The main program remains the same, we just design fact() to invoke itself.

int fact(int input)
{
  if (input == 0 )
    {
      return 1;
    }
  else
    {
      return (input * fact(input - 1));
    }
}

In the recursive version, it is much easier to see the relationship between our definition of factorial and this function's code. If we are trying to find the factorial of 0, return the answer, 1. Otherwise, the factorial of input is input * fact(input - 1). Comments may be superfluous.

To better understand how this recursion works, let us trace the sequence of function invocations and the state of the variables when main() invokes fact() with argument 3.

1. main() invokesfact(3)
2. In fact(), we check if the input paramater is 0, and since it not, we return 3 * fact(2). Before we can return this expression, we have to evaluate fact(2) so that we can do the multiplication. In other words, fact() invokes fact() again, but with argument 2.
3. During this second invocation of fact(), with parameter 2, we again try to return 2 * fact(1), resulting in another invocation of fact()
4. The third time fact() is called, we again try to do the else part and try return 1 * fact(0) causing yet another invocation of fact.
5. The fourth invocation of fact(), with input parameter 0, now causes the then part to be executed, returning a 1.
6. This allows the multiplication in step 4, returning the value 1 * 1 = 1 to step 3.
7. This allows the multiplication in step 3, returning the value 2 * 1 = 2 to step 2.
8. This allows the multiplication in step 2, returning the value 3 * 2 = 6 to step 1.
9. main() prints the value returned from its invocation of fact(3) which is 6.

Going down...           Calculating fact(5) = 5 * fact(4)
Going down...           Calculating fact(4) = 4 * fact(3)
Going down...           Calculating fact(3) = 3 * fact(2)
Going down...           Calculating fact(2) = 2 * fact(1)
Going down...           Calculating fact(1) = 1 * fact(0)
Bottom of recursion...              fact(0) = 1 
doing all multiplications

The factorial of 5 is 120

  if (input == 0 )    /* BAD STYLE */

  if (input <= 0 )	/* GOOD STYLE */

      return (input * fact(input - 1));

      return (input * fact(input - 2));

Back to the Top of this page

Here's another example of recursion. The problem is to sum the numbers from 0 through n. This is very much like the factorial problem except we want to add instead of multiply. The recursive definition of this problem is:

sum(0) = 0 and sum(n) = n + sum(n-1). You should be able to design and implement a function that solves this problem. Here's my version of the answer. You can, of course, write a non-recursive version as well.

For another example, let's define multiplication in terms of repeated addition.

mult(n, 1) = n and mult(n, m) = n + mult(n, m - 1). Now the recursive function will have two arguments but only one of them, the second, changed during the recursion. Here's one version. This version is wrong because it doesn't correctly handle multiplication by 0.

Here's an improved version that handles multiplication by 0. Note that we have two ways of ending the recursion, 1) for handling multiplication by 0, and 2) for handling multiplication by 1. Note also, that the program doesn't handle negative integers.

If you were interested in efficiency you would see that the number of recursive calls depends on the second argument, m. Since multiplication is commutative (n * m = m * n) we can use a helper function to ensure that the second argument is always the smaller one. Here's a third version of multiplication. In the third version, mult() calls multhelper() after putting the arguments in the "correct" order (that is, it puts the smaller number as the second argument).

Back to the Top of this page

Now here's a problem that can be solved recursively. Design a program that will print a string backwards. The first step in designing a recursive program is to define the problem recursively. To do so, we start by finding a stopping condition for the recursion. In this case, if we see a '\0' or NULL character we have reached the end of the string and can stop the recursion. Otherwise we have two choices.

1. We can print the current character and then recurse on the rest of the string, or
2. We can recurse on the rest of the string and then print the current character.

To understand how this program works, I have reproduced it below:

/* Program 7-15: A Third Look at Recursion */

#include <stdio.h>

void print_backwards(char *);

int main(void)
{
   char string[] = "What does this look like backwards.";

   print_backwards(string);
A: puts("");
   return 0;
}

void print_backwards(char * temp)
{
   char hold;
       
   hold = *temp;/* Store one character */
   if ( hold == '\0' )/*If at end of string, stop recursion.*/
        return;
   else
      { 
        print_backwards(++temp);
          /*Recursive call. First moves pointer to next */
          /*character in string.                        */
B:      printf("%c",hold);
          /*Will only be executed on way out of recursion. */
        return;
          /*Continue to undo recursion. */
      }
}

First, there is a piece of memory called the stack associated with each running program. Think of a stack like a box of pringles. You can take chips from the top of the box, you can put in chips at the top of the box, but it is real hard to access chips not at the top. Similarly, in a stack you can put items in the top, or remove items from the top. The C compiler uses the program's stack for storing return addresses and for local variables.

Let's see what happens to the stack as the recursion progresses, and the string "tom" is printed backwards.

In main() we initialize string[] = "tom"; and invoke print-backwards(string). This is invocation 1. At this point, just as with any function, the return address, B is stored on the stack and the program "jumps" to the function print_backwards(). The stack looks like

Next, in print_backwards(), we allocate space for the local variables on the stack. After the hold = *temp statement, the stack looks like:

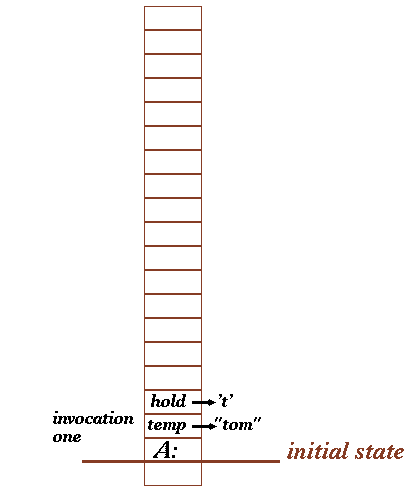
The local variables temp and hold, have been allocated space on the stack, and after hold = *temp, hold contains the character 't', while temp points to the beginning of string "tom".

The if_then_else statement then checks to see if it is the end of the string, since it isn't we invoke print_backwards() again. The argument this time is ++temp, which means first increment the pointer temp and then invoke print_backwards() with this new argument. Incrementing temp makes it point to the string "om", and we are in effect invoking print_backwards("om"). This is invocation 2.

Once again, the return address and local variables are stored on the stack. This time however, the return address is B: since the next statement to be executed is printf("%c",hold);. Skipping ahead, after hold = *temp is executed the second time, the stack looks like

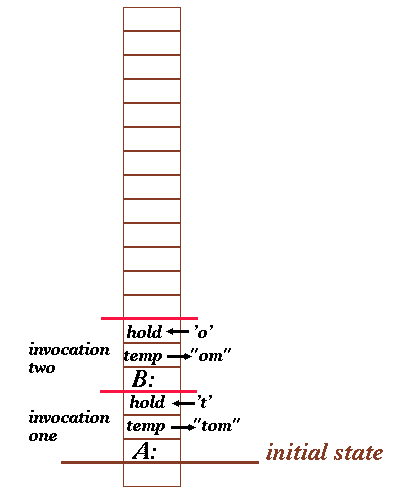
The areas between red lines are called stack frames, each frame corresponds to one function invocation.

Again checking the if_then_else statement, we do the else part which results in the invocation of print_backwards("m"). This is invocation 3. You should be able to predict the contents of the stack after hold = *temp is executed this time around.

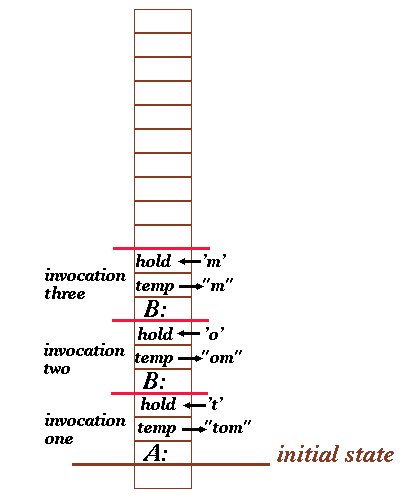
Now, we invoke print_backwards(""), (invocation 4) which passes the empty tring to print_backwards(). After hold = *temp the stack looks like

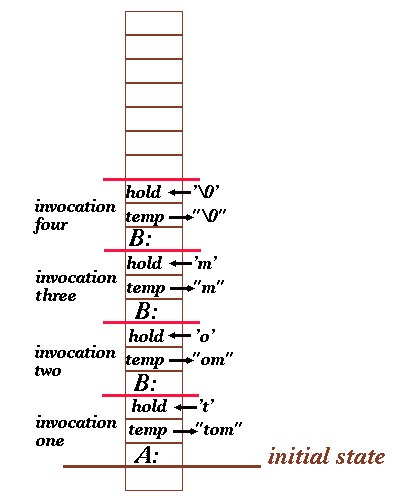
This time, the if_then_else condition is true, and we execute return;. When we return from this function, we destroy the local variables from the stack, pop the return address from the stack and use the return address to tell us which statement to execure next. poping something from the stack removes it from the stack.If we pop the local variables, and the return address, the stack looks like

and we do the statement at B: belonging to the previous invocation (invocation 3) of print_backwards(). This causes us to print the current value of hold which is m, the value of the variable hold in invocation three's stack frame. We then return, causing the local variables to popped from the stack, and the return address used to tell us what to do next.

Since the return address was B: we exit this invocation (the stack looks like this), and execute the print statement of the previous invocation, invocation two. This prints "o" and executes its return.

Local variables are popped from the stack and control returns to the printf statement of the first invocation, causing "t" to be printed. When this invocation executes return, its local variables are popped from the stack, but the return address is now A:, which is the return address of the original call from main(). The stack now looks like it did before the first invocation of print_backwards(), that is, the stack is empty. The return from main causes your program to end.

Whew!