
Table: Test Problems.
Several experiments in function optimization and circuit design show that clustering techniques, if properly applied, provide a strong case-base, yielding useful data about the GA run. A list of problems on which we successfully tested our system is shown in table 1. We also ran a few experiments with the hypothesis module in place.
The tree structure resulting from clustering defines a schema hierarchy [figures 4 and 5]. Schema of lower order are found near the top of the tree. Schema order gets higher and higher towards the leaves, which, with all alleles fixed, have the maximum possible order. Figure 4 depicts the index tree of an entire case-base for a simple function. Some salient features of the space are immediately recognizable on the graph (when one can zoom in and look at cases). We have marked these features in figure 4.
Figure 5 shows an enlargement of the small boxed area in figure 4 (labeled ``Area of Detail''). In this figure, the positions of both initial cases (individuals) to the right of the figure and abstract cases at the internal nodes are represented by their schemas. Schemas closer to the root of the tree are more general (i.e., of lower order) than those towards the leaves.
A Simple Example: f(x)=x
Figure 4 shows the shape of the case-base index for a GA which maximizes the simple function: f(x)=x. The case-base was created by clustering the 400 GA individuals from the first 20 generations (which resulted in a binary tree) and then computing the abstract cases at the internal nodes. The resulting case-base had 799 cases, 400 of which came directly from the GA. By using the report mentioned above in conjunction with the index-tree graph we were able to find the salient features of the search space. We have marked these interesting features on the graph.
Clustering nicely partitions the individuals into sets sharing common features, namely specific allele values (syntactic similarity) and similar fitness. In this case, all the low fitness cases are clumped together toward the top of the graph. The high fitness cases are at the bottom. We included a sign bit in the genotype (values ranged from [-511..511]). The sign-bit branching point is shown in figure 4 as well. Not surprisingly, all the negative numbers are clustered together above the sign-bit branchpoint, and very little time was spent in that portion (half!) of the search space by the GA. This information was discovered by zooming in on the subsections of the graph and noting the obvious common features while consulting the on-line case-base.
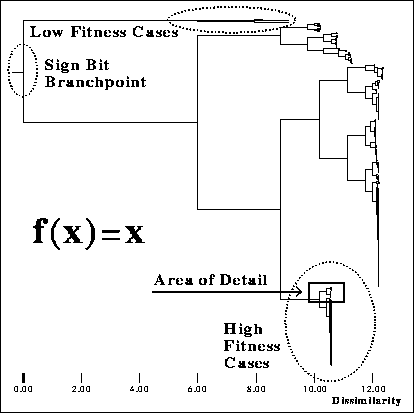
Figure: Tree structure of the cases. Nodes represent abstracted cases.
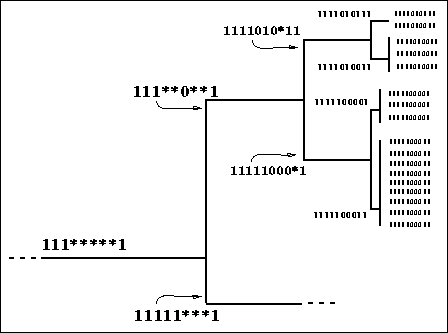
Figure: A closer look at the clustered cases reveals nested schemas.
Case zero is located at the root of the tree. Actual output from a query shows case-information:
> (show-case 0) +--------------------------------------------------------------+ | Case: 0 | Distance: 0 Weight: 400 Fitness: 8441.44 | |------------+ Order: 0 Schema: ********** | | Additive schema: (396 333 170 283 338 330 20 72 332 392) | | Longevity: 19 (lo:1 avg:10.5 hi:20) | | Left subtree: 1 Right subtree: 396 | +---------------------------------------------------------------
Since case 0 is located at the root of the tree, its distance from the root is 0. There are 400 leaves below it, making its weight 400. Fitness is calculated by averaging the fitnesses of the cases below. The case schema is filled with ``*''s, showing once again why the additive schema information is important. Leaves under case 0 spanned all generations from 1 to 20 resulting in a longevity value of 19. Case 0 has two pointers, one to case 1 and another to case 396. This reflects the binary nature of the index. Had the case been a leaf it would not have pointed to further cases.
We tested several very simple functions in order to discover just how much information the case-base can provide about the problem space. Salient features are apparent from the structure of the graph. This tendency could prove to be important in understanding black box fitness functions.