We tested our system on the combinational circuit design
problem. This problem's search space is poorly understood,
discontinuous, and highly non-linear. The problem can be stated as
follows: given a set of logic gates to work with, design a circuit
that performs a desired function. One instantiation of this problem
is a parity checker, a circuit that returns the parity of a
fixed number of bits (Louis and Rawlins 1991). When encoded for the
GA, a 5-bit parity checking problem results in a 
sized
search space having the troublesome properties listed above. We used a
genotype of length 80, a population size of 20 and ran the GA for
25 generations. A candidate design is evaluated for fitness by
testing a simulation on all possible inputs.
The GA does not solve the problem in 25 generations. In our experiments, a case-base was created by clustering the 500 individuals created by the GA and computing the 499 abstract cases. After examining the report and following the steps outlined in the methodology section, we examined the disjoint subtree list. The strongest such subtree (H) was also heavily weighted and spanned many generations. In addition, the best partial solutions all fell within H. We therefore suspected that a complete solution would fit H's schema. Since the order of the schema was appreciable (53 of 80), we could constrain the search to that schema and still hope to find a solution. The solution was in fact contained in H's schema.
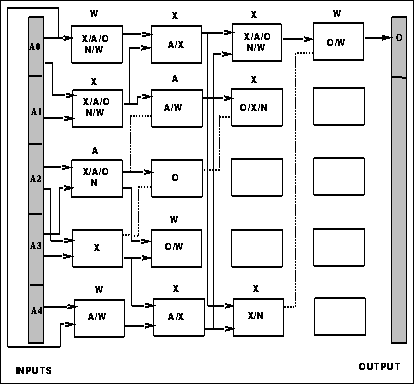
Figure: Parity circuit indicated by H, and the correct instantiation of
choices.
Figure 6 shows the circuit indicated by our analysis of H. By
decoding H, we were able to discern the general structure of a
solution and determine which parts of it were important. The
unlabeled boxes represent unimportant dimensions of the search space
which can be safely ignored. Labeled boxes represent one of the logic
gates eXclusive-or, And, Or, Not, and
Wire. Since we are drawing the circuit represented by a schema,
multiple labels on the boxes show its possible instantiations. Labels
above boxes represent a correct instantiation found near the 
generation of an unconstrained run. The top row should be considered
adjacent to the bottom.