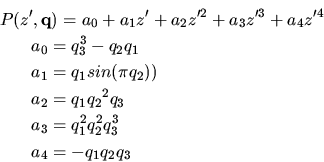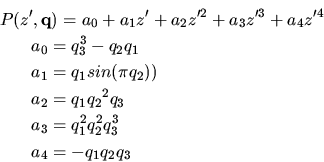Next: Conclusions
Up: Results
Previous: Example 2
We now consider a simple example that has been specifically constructed to
mislead the genetic algorithm approach. Consider a fourth order
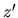 polynomial
polynomial
The system's uncertain parameter ranges are
![$Q = \{ {\bf q}: \: q_1\in[1.4;
3.0], \: q_2\in[1.0; 2.8], \: q_3\in[1.8; 3.2], \: q_4\in[1.2; 2.8]\}$](img73.gif) .
We
constructed this polynomial to stress that our approach only provides
sufficiency conditions. A genetic algorithm using the same GA parameters as in
the previous two examples was unable to find any roots on or within the unit
circle even after 1000 generations. We thus cannot conclude anything about
the system's stability from our approach and will need to use some other tool
for stability analysis - in this case, an analytic solution is possible.
.
We
constructed this polynomial to stress that our approach only provides
sufficiency conditions. A genetic algorithm using the same GA parameters as in
the previous two examples was unable to find any roots on or within the unit
circle even after 1000 generations. We thus cannot conclude anything about
the system's stability from our approach and will need to use some other tool
for stability analysis - in this case, an analytic solution is possible.
Sushil Louis
1998-10-23