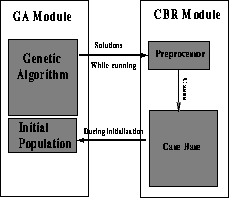
Figure 1: Conceptual view of our system
Combining genetic algorithms with a long term memory model, like case-based reasoning, combines the strengths of both approaches. The case-base does what it is best at -- memory organization; the genetic algorithm handles what it is best at -- adaptation. The resulting combination takes advantage of both paradigms; the genetic algorithm component delivers robustness and adaptive learning while the case-based component speeds up the system. Furthermore, in many application areas we confront sets of similar problems. It makes little sense to start a problem solving search attempt from scratch with a random initial population when previous search attempts may have yielded useful information about the search space. Instead, seeding a genetic algorithm's initial population with solutions to similar previously solved problems can provide information (a search bias) that, hopefully, increases the efficiency of the search. If no useful information was obtained or obtainable, a randomly initialized population may be our only choice. Our approach borrows ideas from case-based reasoning (CBR) in which old problem and solution information, stored as cases in a case-base, help solve a new problem [12]. Although we restrict ourselves to genetic algorithms in this paper, we should be able to substitute, with minor modifications, any population based search algorithm for the genetic algorithm. We believe that evolutionary programming, genetic programming, and evolution strategies are especially suitable. Figure 1 shows a conceptual view of a first version of our system.

Figure 1: Conceptual view of our system
Previous work in this area includes Louis, McGraw, and Wyckoff's paper that applied Case-Based Reasoning (CBR) to GAs as an analysis tool for the parity combinational circuit design problem [7]. Ramsey and Grefensttette seeded a genetic algorithm's initial population with cases and reported improved performance on the non-stationary functions that they used [11]. More recent work by Louis, Liu, and Xu addresses the questions of which cases are ``appropriate'' and how many cases to inject [6, 9] and establishes the feasibility of the method using the open-shop scheduling and rescheduling problem and the combinational circuit design problem.