In the first three experiments, we use CHC without scaling and the entire
initial population is randomly generated. The threshold for the Hamming
distance is ( 
as is the norm for
CHC. Scaled CHC is used to overcome the possible monopoly of solutions with
extremely high fitness (caused by injection) in the complex environment.
The fitness functions that were used are shown below:
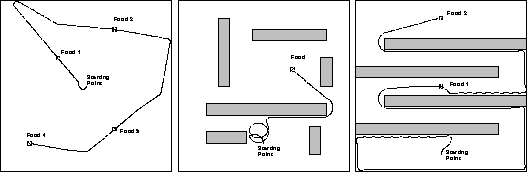
Figure 3: The simbot's path when learning food approach (left),
obstacle avoidance (middle), and wall following (right) behavior
CHC proved to be a reasonable and effective method for designing basic control strategies for a simbot. As shown in Fig 3, the simbots have successfully evolved the expected basic behaviors of food approach, obstacle avoidance, and wall following. This figure depicts the paths taken by the best individual for each of these first three experiments. Note that the control circuits may not be optimal.
In the next set of experiments we designed the control strategies of a simbot in a complex office environment by injecting a suitable number of appropriate cases into the GA's initial population. First, we copied one case corresponding to the best individual for a basic behavior from each of the first three experiments for a total of three cases. Second, five cases were selected from the best 30 candidates of the first three experiments' results according to the candidates' fitness values in the office environment. We found that injecting five cases produced better performance than injecting a larger or smaller number of cases. We believe, that injecting a larger number of cases leads to insufficient exploration and injecting a fewer number of cases leads to insufficient exploitation. Five percent is a happy medium. We call the GA injected with these cases the Target Ranked Genetic Algorithm or TR-GA, and the GA injected with the best cases in the basic behavior environments the Source Ranked Genetic Algorithm or SR-GA. We also ran the GA with a randomly initialized population (RI-GA) for comparison purposes.
The maximum performance curves over 10 runs of the genetic algorithm are shown in Fig. 4.
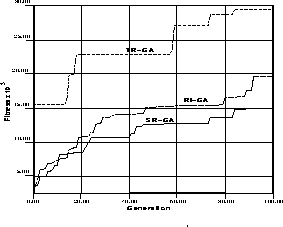
Figure 4: The genetic algorithm maximum performance curves
As we can see, the TR-GA significantly out-performed its competitors. Although Fig. 4 compares a TR-GA with five injected individuals to a SR-GA that used three injected individuals, the TR-GA with three injected individuals also did better than the SR-GA, while not doing as well as the TR-GA with five. Somewhat surprisingly the randomly initialized GA did better than the SR-GA, indicating that the best control strategies for basic behaviors may not contain building blocks that help navigation in the office environment and/or may be of low enough fitness to be eliminated during GA processing. More evidence is presented in Table 2 which compares the fitness, in the office environment, of cases injected into the SR-GA with those injected into the TR-GA. We also noted that solutions with high initial fitness in the target office environment may be ranked low in their source environment.
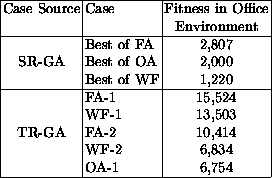
Table 2: Cases used for SR-GA and TR-GA and their fitness in the office
environment. FA = food approach, WF = wall following, OA = obstacle avoidance.
The results indicate that injecting appropriate cases into the initial
population of a genetic algorithm can not only help speed up convergence but
also provide better quality solutions. However, this will only work if injected
solutions contain useful building blocks for solving the new problem, that is,
if injected solutions are similar enough to solutions for the new
problem. Assuming that problem similarity implies solution similarity is a
pre-requisite for our system to perform well [6, 9], but when
trying to combine several solutions, we had to re-validate this assumption by
evaluating and ranking candidates for injection in the new target
environment. Previous results had not indicated the need for ranking cases in
the new environment before injection [6]. However, we obtained good
agreement in our estimate of the number of individuals to inject. Earlier work
had shown that injecting only a small percentage of the population led to
good performance while injecting larger percentages led to quick convergence
to a local optimum [6]. This agreed with the experimental
results reported in this paper where we found that injecting five individuals
( 
of the population) provided better performance compared to experiments
involving the injection of a smaller or larger number of individuals.
In addition, we need to make sure that the injected individuals contain at least one representative of each basic behavior. Otherwise, the missing basic behavior may have to be evolved from scratch - from the randomly initialized component of the population. Once we have individuals representing each of the basic behaviors, the rest of the candidates for injection compete for the remaining slots on the basis of their performance in the target environment. This ensures that the population is initialized with the needed variety of high performance building blocks.
Figure 5 presents the path of a simbot, controlled by a circuit
designed by the TR-GA, in the office environment. Note that although the
environment contains many traps in the form of rooms with small doorways, the
simbot does not get trapped and manages to avoid two unpromising rooms
altogether. The TR-GA designed simbot also eats 
of the food
over ten runs compared to only 
for the randomly initialized GA.
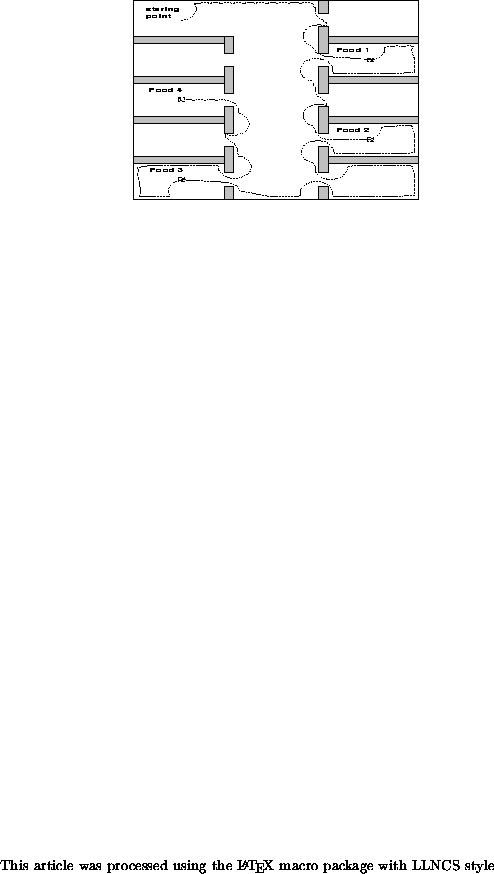
Figure 5: Simbot path in an office environment for a circuit designed by the
TR-GA