Figure 3: Traditional crossover is not suitable for TSPs
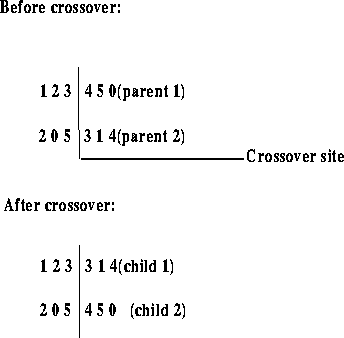
Because of our representation, the traditional crossover and mutation operators are not suitable for TSPs. Figure 3 shows that traditional crossover produces illegal children. The first child is illegal because city 1 and city 3 appear twice, while city 0 and city 5 do not appear at all. The second child is also illegal because city 0 and city 5 appear twice, while city 1 and city 3 do not appear.
There are several crossover operators for TSPs. We use Greedy Crossover which was invented by Grefenstette [Grefenstette 85] in 1985. Greedy crossover selects the first city of one parent, compares the cities leaving that city in both parents, and chooses the closer one to extend the tour. If one city has already appeared in the tour, we choose the other city. If both cities have already appeared, we randomly select a non-selected city.
For example, if we have two parents
1 2 3 4 5 0
4 1 3 2 0 5
To generate a child using the second parent as the template, we select city 4 (the first city of our template) as the first city of the child.
4 x x x x x
Then we find the edges after city 4 in both parents: (4, 5) and (4, 1) and compare the distance of these two edges. If the distance between city 4 and city 1 is shorter, we select city 1 as the next city of child 2.
4 1 x x x x
Then we find the edges after city 1 (1, 2) and (1, 3). If the distance between city 1 and city 2 is shorter, we select city 2 as the next city.
4 1 2 x x x
Then we find the edges after city 2 (2, 3) and (2, 0). If the distance between city 2 and city 0 is shorter, we select city 0.
4 1 2 0 x x
The edges after city 0 are (0, 1) and (0, 5). Since city 1 already appears in child 2, we select city 5 as the next city.
4 1 2 0 5 x
The edges after city 5 are (5, 0) and (5, 4), but city 4 and city 0 both appear in child 2. We select a non-selected city, which is city 3. and thus produce a legal child
4 1 2 0 5 3
We can use the same method to generate the other child.
1 2 0 5 4 3
After crossover, both offspring encode legal tours.