Genetic Algorithms

A genetic algorithms is a search algorithm based on the mechanics of natural selection and natural genetics and is used to search large, non-linear search spaces where expert knowledge is lacking or difficult to encode and where traditional optimization techniques fall short [Goldberg 89]. The basic principles of GAs were first designed by John Holland [Holland 75]. A genetic algorithm works with a population of individual strings (chromosomes), each representing a possible solution to a given problem. Each chromosome is assigned a fitness value according to the result of the fitness function. Highly fit chromosomes are given more opportunities to reproduce and the offspring share features taken from their parents.

GAs are different from other optimization and search procedures in four ways  [Goldberg 89]:

1. A GA works with a coding of the parameter set, not the parameters themselves.
2. A GA searches from a population of points, not a single point. The search is carried out from generation to generation until convergence.
3. A GA uses payoff information, not derivatives or other auxiliary knowledge. The value of an objective function feeds back to direct a search.
4. A GA uses probabilistic transition rules, not deterministic rules. The best fitness value is not guaranteed to be found, but a GA usually makes significant progress.

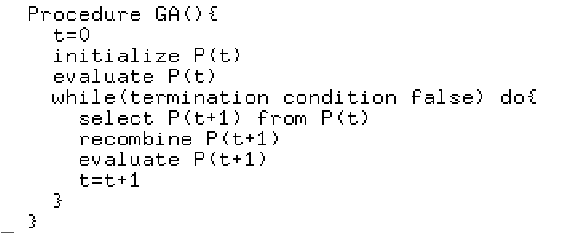
GAs generally consist of three operators: selection, crossover and mutation. Suppose P(t) is the population of strings at generation t, the structure of a simple GA is as follows:

 

Evaluation of each chromosome determines which is better based on a fitness function. Selection is a process in which individual strings are copied according to their fitness function value. The traditional GA uses a selection where the probability of selection is proportional to the fitness value (roulette wheel selection); highly fit individuals have a higher probability of being selected for further processing. Recombination includes two operators, crossover and mutation. The traditional crossover operator randomly chooses a crossover cite, cuts chromosomes into two substrings, and swaps the tail substrings to produce two offspring chromosomes as shown in Figure 1.

  
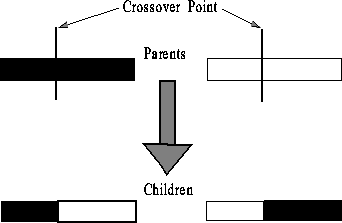
Figure 1: Traditional Crossover operator

Mutation changes the value of a single bit and helps prevent being stuck on a local optimal. The traditional mutation operator randomly chooses a bit and changes the bit from 1 to 0 or 0 to 1 as shown in Figure 2.

  
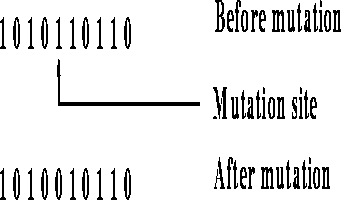
Figure 2: Traditional Mutation Operator