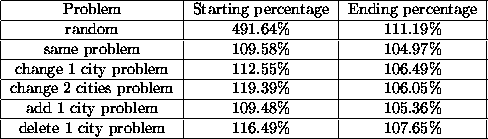
Table 3: Average distance from optimal for all problems
Table 5 compares the average performance across all our TSP problems. Column one specifies how we modified the original problem, while column two and three show the percentage distance of the first and the last generation tour length from the optimal tour length. From this table, we can see that after injecting individuals and running GAs with previous information, we can always get better results than when running GAs with random initialization on our problems.

Table 3: Average distance from optimal for all problems
We provide details on each modified problem and use performance graphs on the 76 cities TSP to illustrate our results. Performance figures for the rest of the TSP problems are available in the Appendix.
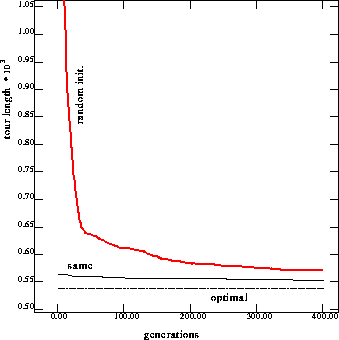
Figure 7: Performance on 76 cities problem with injection from solutions
to the same problem
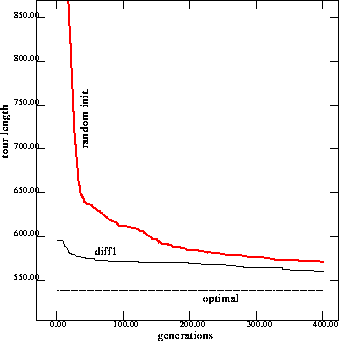
Figure 8: Performance on 76 cities problem with injection from solutions
to the changing one city problem
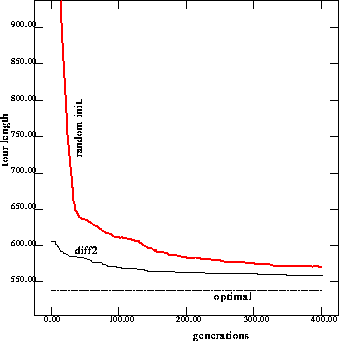
Figure 9: Performance on 76 cities problem with injection of solutions to
the changing two cities problem
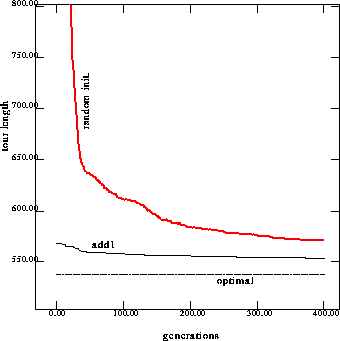
Figure 10: Performance on 76 cities problem with injection from solutions to the
adding one city problem
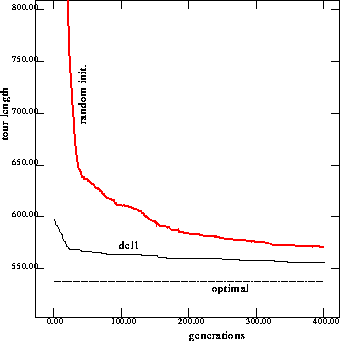
Figure 11: Performance on 76 cities problem with injection from
solutions to the deleting one city problem
Figure 12 and Figure 13 show the optimal solution [Reinelt 96] and our best solution by running the NRGA on the 76 cities TSP. The edges are not all the same, but the lengths are very close
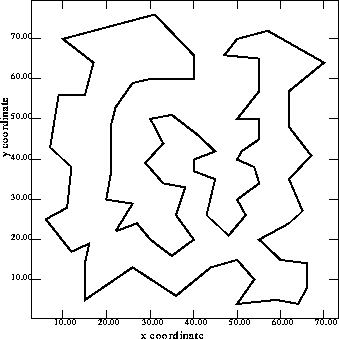
Figure 12: Best solution of 76 cities TSP. Tour length = 538
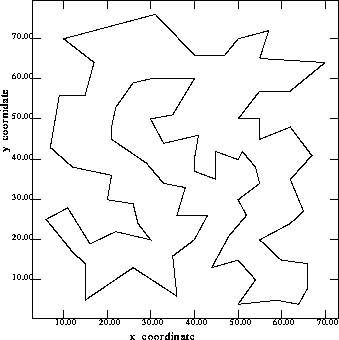
Figure 13: Our best solution of 76 cities TSP with previous information. Tour length = 549
As Table 5 shows, after injecting solutions of previous similar problems, the performance is always better than running the GA with random initialization.
When using the GA to solve TSPs, the absolute location of a city in a string is less important than the relative location of a city with respect to a tour. For example, for a 3 cities tour, (1 2 0) and (0 1 2) mean the same tour. However, pairs of cities, that is edges, are now important. We believe the reason we can always get good performance during early generations after injecting individuals and running NRGAs with previous information is that those injected individuals contain good edges from similar problems. The combined system (GAs + CBR) is able to learn and remember good partial tours and thus takes less time to solve a new problem.
Short, highly fit subsets of strings (building blocks) play an important role in the action of genetic algorithms because they combine to form better strings [Goldberg 89]. Edges are important in creating building blocks for the traveling salesman problems. After we inject individuals contain good edges, learned from solving similar problems, the NRGA can combine these good edges and quickly approach the optimum. This may explain why changing problem size by adding a city still results in better performance compared to deleting a city. Our results show that injecting individuals from the same problem and the add1 problem can help the NRGA get better performance than when injecting individuals from other problems. In both these cases, we use information from all cities and the length of each edge remains the same. This implies that a different sized problem with information from all cities and all edges can help the NRGA get better performance than a same sized problem with some different edges.