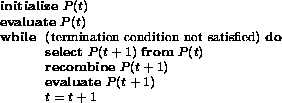
This paper describes a system for explaining solutions generated by genetic algorithms (GAs) using tools developed for case-based reasoning (CBR). In order to make this paper accessible to researchers who may not know about both CBR and GAs, we have included two introductory subsections explaining each in basic terms. Subsections 1.1 and 1.2 may be skipped without loss of continuity.
A genetic algorithm (GA) is a randomized parallel search method based on evolution. GAs have been applied to a variety of problems and are an important tool in machine learning and function optimization. David Goldberg's book gives a thorough introduction to GAs and provides a list of possible application areas (Goldberg 1989). The beauty of GAs lies in their ability to model the robustness and flexibility of natural selection.
In a classical GA, each of a problem's parameters is represented as a binary string. Borrowing from biology, an encoded parameter can be thought of as a gene, where the parameter's values are the gene's alleles. The string produced by the concatenation of all the encoded parameters forms a genotype. Each genotype specifies an individual which is in turn a member of a population. An initial population of individuals, each represented by a randomly generated genotype, is created. The GA starts to evolve good solutions from this initial population. The three basic genetic operators: selection, crossover, and mutation carry out the search. Genotypic strings can be thought of as points in a search space of possible solutions. They specify a phenotype which can be assigned a fitness value. Fitness values affect selection and in this way guide the search.
Selection of a string, depends on its fitness relative to that of other strings in the population. The genetic search process is iterative: evaluating, selecting, and recombining strings in the population during each iteration (generation) until reaching some termination condition. The basic algorithm, where P(t) is the population of strings at generation t, is:
Evaluation of each string (individual) is based on a fitness function that is problem dependent. This corresponds to the environmental determination of survivability in natural selection. Selection is done on the basis of relative fitness. It probabilistically culls from the population individuals having relatively low fitness. Mutation flips a bit with very low probability and insures against permanent loss of alleles. Crossover fills the role played by sexual reproduction in nature. One type of simple crossover is implemented by choosing a random point in a selected pair of strings (encoding a pair of solutions) and exchanging the substrings defined by that point. Figure 1 shows how crossover mixes information from two parent strings, producing offspring made up of parts from both parents. This operator which does no table lookups or backtracking, is very efficient because of its simplicity. One-point crossover, where A and B are the two parents, producing two offspring C and D, is shown in figure 1.
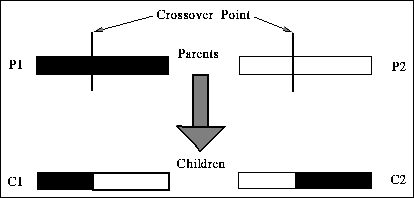
Figure: Single-point crossover of the two parents A
and B produces the two children C and D. Each child consists of parts
from both parents leading to information exchange.
The individuals in the population act as a primitive memory for the GA. Genetic operators manipulate the population, usually leading the GA away from unpromising areas of the search space and towards promising ones, without the GA having to explicitly remember its trail through the search space (Rawlins 1991).
It is easiest to understand GAs in terms of function optimization. In such cases, the mapping from genotype (string) to phenotype (point in search space) is usually trivial. For example, in order to optimize the function f(x)=x, individuals can be represented as binary numbers encoded in normal fashion. In this case, fitness values would be assigned by decoding the binary numbers. As crossover and mutation manipulate the strings in the population thereby exploring the space, selection probabilistically filters out strings with low fitness, exploiting the areas defined by strings with high fitness.
Since crossover causes genotypes to be cut and spliced, it is impractical to consider or track individual strings in analyzing a genetic algorithm. Instead, the analysis must focus on substrings which define regions of the search space and are called schemas. The schema theorem will be discussed in subsection 1.3.
Case-based reasoning (CBR) embraces the idea that reasoning and explanation can best be done with reference to prior experience, stored in memory as cases. The approach de-emphasizes reasoning from first principles. The strategy is first to amass and index a large and varied collection of examples, then, when presented with a new situation, to fetch and possibly manipulate the stored example which most closely resembles the new situation. Each stored case may be considered a previously evaluated data point, the nature and location of which is problem dependent. If the distance metrics have been well designed and the case-base includes sufficient variety, retrieved cases reveal useful conclusions from previous analysis. Because it may be impractical to store all prior experience in detail, CBR systems often include principled mechanisms for generalization and abstraction of cases. Note that except when comparing distinct cases, a CBR system need not include any notion of an underlying model, and that even during comparison one can make do without much of one. A great strength of the approach is that the generalizations and abstractions may in fact induce a useful domain model.
Genetic algorithms (GAs), invented by John Holland in the early seventies, provide an efficient tool for searching large, poorly understood spaces often encountered in function optimization and machine learning (Holland 1975). GAs model natural selection, implemented through selection, recombination and mutation operators.
The probabilistic nature of GA search allows GAs to be successfully applied to a variety of NP-hard problems (Goldberg 1989; DeJong and Spears 1989; Jones and Beltramo 1991). The population-based, emergent nature of computation in GAs lends them a degree of robustness and flexibility that is often unobtainable using vanilla expert systems approaches. This fact has encouraged researchers to apply GAs to creative design tasks such as the design of semiconductor layout, aircraft engine design, and circuit design (Shahookar and Mazumder 1990; Bramlette and Cusic 1989; Louis and Rawlins 1991). This is not to say that GAs currently hold the answer to machine learning! The scarcity of GA theory is an alarming stumbling block in the way of progress.
Holland's schema theorem is fundamental to the theory of genetic algorithms. A schema is a template that identifies a subset of strings with similarities at certain string positions. For example, consider binary strings of length 6. The schema 1**0*1 describes the set of all strings of length 6 with 1's at positions 1 and 6 and a 0 at position 4. The ``*'' is a ``don't care'' symbol which means that positions 2, 3 and 5 can have a value of either 1 or 0. The order of a schema is defined as the number of fixed positions in the template, while the defining length is the distance between the first and last specific positions. The order of 1**0*1 is 3 and its defining length is 5. The fitness of a schema is the average fitness of all strings matching the schema. Remember that the fitness of a string is a measure of the value of the encoded problem solution, as computed by a problem-specific evaluation function. With the genetic operators as defined above, the schema theorem states that short, low-order, schemas with above average fitness increase exponentially in successive generations. Expressed as an equation:
![]()
Here m(h,t) is the number of schemas h at generation t, f(h)
is the fitness of schema h and ![]() is the average
fitness at generation t. The probability of disruption is the
probability that crossover or mutation will destroy the schema h.
is the average
fitness at generation t. The probability of disruption is the
probability that crossover or mutation will destroy the schema h.
The building block hypothesis (BBH), which follows from the schema theorem, can be stated as follows:
A genetic algorithm seeks near-optimal performance through the juxtaposition of short, low-order, high performance schemas or building blocks (Goldberg 1989).Since both the order and defining length are syntactic measures, the BBH implies that syntactically-similar (short and low-order), high-performance individuals bias genetic search. This bias is achieved through the proliferation of specific nontrivial features of strong individuals.
Unfortunately, GA theory tells us little about the actual path a given GA will take through a space on its way to an answer. Because of the stochastic nature of GA operators, a solution's optimality is often suspect and its building blocks unknown.
Information about the building blocks is implicit in the processing done by a GA but is not documented explicitly or available to the user. At convergence, solutions may therefore be opaque, diluting confidence in the results and making analysis difficult. Keeping track of historical regularities and trends is key to acquiring the knowledge needed to explain post facto what sort of solution evolved, why it works, and where it came from. Discovery of building blocks allows principled partitioning of the search space. Empirical regularities can be formalized and possibly put to use. As noted in the GA introduction, genetic algorithms by their very nature trade the use of explicit memory for the speed and simplicity won by its omission. We use the methods and tools developed for case-based reasoning (Bareiss 1991; Riesbeck and Schank 1989) to extract, store, index and later retrieve information generated by a GA.
Case-based reasoning (CBR) provides a method of gathering knowledge in the form of cases (usually built from examples), indexing it in a meaningful fashion, and adapting it to hypothesize about the world. Individuals created by the GA provide a set of initial cases from which a well-structured case-base can be constructed. The BBH points to the use of fitness and genotype as metrics for indexing the case-base. These measures provide the key to indexing the cases and conveniently solve one of the hardest of CBR problems. For our system to work properly, the assumptions of the BBH must be true. Our working system provides empirical evidence in support of the building block hypothesis.
We apply CBR to GAs as an analysis tool in order to track the history of a search. The CBR system creates a case for each individual that the GA has evaluated. These cases are indexed on syntactic similarity and fitness. When properly formed and analyzed, this case-base can contribute to the understanding of how a solution was reached, why a solution works, and what the search space looks like. At the interruption (or termination) of a GA run, the case-base allows the interpretation and subsequent modification of discovered solutions.
If the system digests enough information during a run, it may be able to generate hypotheses about the space that are largely correct. Given proper hypothesis formation, the CBR module can guide the evolution more directly towards convergence. The existence of false hypotheses provides supporting evidence of deception in the current search space.
Our prime motivation is to be able to explain (in an automatic way) the why of an evolved phenotype. Such a tool can be used to attack the following problems: