Example 1

Consider the following $z^{\prime}$ polynomial

$$\begin{eqnarray*}\lefteqn{ P(z^{\prime}, {\bf q}) = a_0 + a_1z^{{\prime}} + a_2... ... \\ & & a_3 = -q_2^2 \\ & & a_4 = q_1 \\ & & a_5 = q_1+q_2 \end{eqnarray*}$$

with $Q = \{ {\bf q}: \: q_1\in[0.5; 1.0], \: q_2\in[0.8; 1.5], \: q_3\in[0.4; 1.2], \: q_4\in[0.5; 1.0],\: q_5\in[0.8; 1.7]\}$. The coefficients of polynomial include affine, multilinear, quadratic and trigonometric terms.

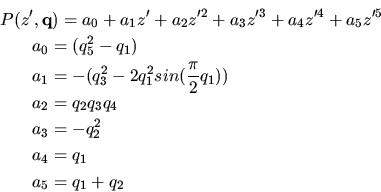
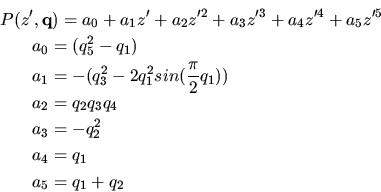
The result given in Figure 7 demonstrates the fitness value of an uncertain polynomial found by the GAs as a function of generation. We set the tolerance $\epsilon$ equal to $9 \times 10^{-16}$ as a true numeric zero. The GA stopped when its fitness reaches $\epsilon$. From Figure 7, although the fitness profile barely (visibly) changes after the 40th generation, the GA continuously takes tiny steps to approach a final optimal solution. After running 226 generations, the GA found a pair of roots on the unit circle for $P(z^{\prime },{\bf q})$ at |1.0|e^{2.84317337937836980j} with
${\bf q}:[0.998697534807558,1.492783030649645$, 0.424252720951437, 0.982848197210973, 0.808143979297398]^T
and $P(z^{\prime},{\bf q}) = 5.551\!E\!-\!17 \pm 4.441\!E\!-\!16j$. Since the accuracy is far beyond our requirement, we can safely conclude that there is a root on the unit circle and that the given polynomial $P(z^{\prime },{\bf q})$ is unstable. The computation time required is less than a minute on a Pentium 200 machine.

Although detecting a root on the unit circle is sufficient to conclude the search, we continued searching for roots inside the unit circle. The GA detected a pair of roots at |0.99448845954136977|e^{0.65541191108445074j}after 498 generations. Obviously, searching for roots on the unit circle is more efficient than searching inside the unit circle. In this example, GAs worked well for testing the sufficient condition of instability for nonlinear uncertain systems with a given accuracy.

  

Figure: The fitness of the polynomial $P(z^{\prime },{\bf q})$ as function of generation (Example 1)

It is interesting to visualize how the uncertain parameter is evaluated by the GA. Figure 8 shows changes in the uncertain parameter family during the evolution process. The value of parameters in each generation sways severely in an early short period. It then advances forward to the true root by taking very fine step changes. The GA searches fit structures in the uncertain parameter Q space and moves toward the global optimum by gradually reducing the chance of reproducing unfit structures, as shown in Figure 8. Unlike gridding techniques, which leads to a combinatoric explosion in the parameter domain, GAs search a much smaller set of structures based on natural selection, and save enough computation time to make a search based approach feasible for this problem.

  

Figure: The uncertain parameter space Q of $P(z^{\prime },{\bf q})$ as a function of generation