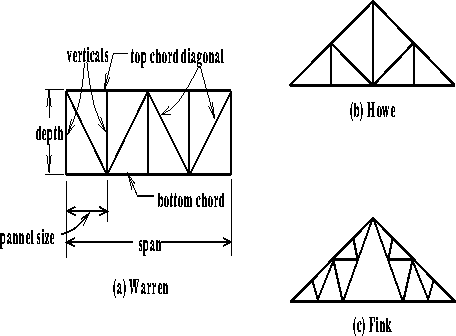
Figure 1: Three Different Types of Trusses
A truss is a structure that consists of a set of long, slender members arranged in the shape of one or more triangles (see figure 1). The members are assumed to be connected by frictionless pins and external loadings are applied only at the truss joints. Truss design usually starts with a given distance that the structure has to span and the loading conditions. Next, the designer determines the depth and overall profile of the truss (geometry), the number of members and their arrangement (topology), and the shape and areas of member cross sections (component properties) such that the truss will be able to resist the given loads while meeting the service requirements (specifications). The goal of truss optimization is to maximally utilize the material to result in the lightest structure while satisfying all the design, manufacturing, and other physical constraints.

Figure 1: Three Different Types of Trusses
Traditionally, truss optimization is performed using mathematical optimization techniques for a truss with a fixed configuration. That is, given the geometry and topology, the truss member cross sectional areas are optimized. The task, although well formulated, involves intensive computation. Using mixed integer optimization techniques, limited topology optimization may be achieved based on a set of alternative fixed configurations. An example of applying GAs to truss member optimization is reported in [Goldberg, 1989]. Jenkins also applies a GA to optimize truss geometry and member cross sectional areas [Jenkins, 1991]. In his study the topology is fixed and geometry is defined by a set of parameters such as member lengths and their inclined angles. To our knowledge, the only reported attempt on optimization of truss topology is described in Cagan and Mitchell's work [Cagan and Mitchell, 1993], in which simulated annealing (a search algorithm) is used to search through possible truss topologies. A truss topology is first generated by a shape grammar producing a triangularized shape. The geometry is then adjusted to satisfy problem constraints (the locations of supports and loads), followed by shape optimization based on, for example, stress, buckling, and manufacturing constraints using traditional optimization techniques. Based on the utility of the resultant shape the simulated annealer searches for another shape and the whole process is repeated. One problem with this approach, as pointed out by the authors, is that a complete shape optimization is performed at each step. This takes significant computational time, especially if the truss is statically indeterminate. The internal force distribution in a statically determinate truss, or any such structure in general, may be calculated independently of the members' properties while its calculation in a statically indeterminate structure requires information about members' properties, which are themselves the targets of optimization.
Genetic algorithms have also been used in shape design [Gero et al., 1994, Watabe and Okino, 1993]. Although shape grammars provide a powerful representation technique, we chose a different representation for reasons of computational complexity and because we found it difficulty to encode heuristic (engineering design) knowledge. Our representation is described in Section 5 while the next subsection introduces genetic algorithms.
Genetic algorithms, originally developed by Holland, model natural selection, the process of evolution [Holland, 1975]. Conceptually, GAs use the mechanisms of natural selection in evolving individuals that, over time, adapt to an environment. They can also be considered a search process, searching for better individuals in the space of all possible individuals. In practice, individuals represent candidate designs in a state space of possible designs, while the environment provides a measure of ``fitness'' that helps identify better individuals. Genetic algorithms are a robust, parallel search process requiring little information to search effectively. Goldberg's book provides a large list of application areas [Goldberg, 1989].
As already noted, the motivational idea behind GAs is natural selection implemented through selection and recombination operators. A population of candidate designs (usually encoded as bit strings) is modified by the probabilistic application of the genetic operators from one generation to the next. The basic algorithm where P(t) is the population of strings at generation t, is given below.
t = 0initialize P(t)
evaluate P(t)
while (termination condition not satisfied) do
begin
select P(t+1) from P(t)
recombine P(t+1)
evaluate P(t+1)
t = t+1
end
Evaluation of each string which encodes a candidate design is based on a fitness function that is problem dependent. This corresponds to the environmental determination of survivability in natural selection. For our problem, a finite element analysis program calculates the total weight, node displacements, and member stresses, providing the information necessary for evaluating a design.
Selection is done on the basis of relative fitness and it probabilistically culls from the population those designs that have relatively low fitness. Recombination, which consists of mutation and crossover, imitates sexual reproduction. Mutation, as in natural systems, is a very low probability operator and just flips a specific bit. Crossover in contrast is applied with high probability. It is a structured yet stochastic operator that allows information exchange between candidate solutions. Two point crossover is implemented by choosing two random points in the selected pair of strings and exchanging the substrings defined by that point. Figure 2 shows how crossover mixes information from two parent strings, producing offspring made up of parts from both parents. We note that this operator, which does no table lookups or backtracking, is very efficient because of its simplicity. In summary, selection concentrates search in promising areas of the search space, while crossover and mutation provide new points in the search space (solutions) to evaluate. We can think of a genetic algorithm as a population of information exchanging hill climbers.
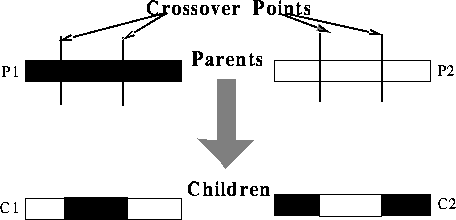
Figure 2: Crossover of the two parents A and B produces the two
children C and D.
Holland's fundamental theorem of genetic algorithms, the schema theorem, leads to the building block hypothesis which states that genetic algorithms work near-optimally by combining certain types of building blocks corresponding to partial solutions or designs [Goldberg, 1989]. In terms of truss design, genetic algorithms can be expected to combine good parts of candidate structures to generate improved structures.
The next section describes our methodology, the representation of the space of possible trusses, and how knowledge is encoded in the representation and genetic operators. The genetic algorithm searches this space for a feasible truss that optimizes weight, nodal displacement, and member stresses.