REPRESENTATION

 

The first engineering heuristic that we encode indicates that good values for truss depth lie between 1/12 and 1/8 of the span for Warren trusses. Providing some leeway, we initialize the population by randomly generating trusses with depths between 1/14 and 1/6 of the span. Thus we determine initial truss depths with the following formula

where generates a random number between x and y inclusive.

The panel size heuristic suggests that panels be of approximately the same size as the depth. Thus trusses in the initial population have approximately equal depths and panel sizes.

Members are now generated to connect nodes such that the profile is, with high probability, triangularized. Triangularization makes for stable trusses. If we consider a rectangular truss to be made of two chords, top and bottom, we start with the leftmost node in the top chord and generate between 2 and 5 members to connect to adjacent nodes. Step 0 in Figure 3 shows that 3 members have been generated from node [1,0] to nodes . There is already one triangular structure, but one member ([1,0]-[1,1]) has been left dangling. In the next step, we connect node [1,1] with other nodes. This time we have generated (randomly) 4 members connecting to the nodes . We continue in this way until reaching the rightmost node, in this case node [1,5]. At this point, if a node does not form the vertex of a triangle, we add bracing members to triangularize the structure. This results in the truss structure shown at the bottom of figure 3.

  
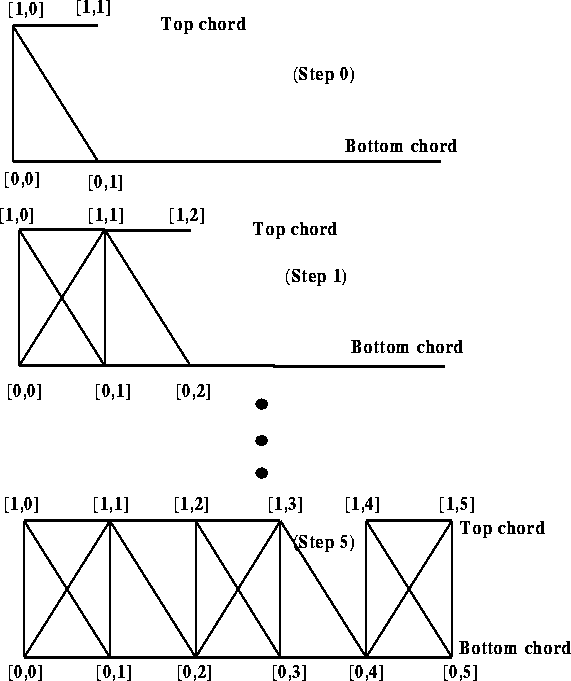
Figure 3: Generating a truss in the initial population.

Each member's cross sectional area is generated randomly in the range between 0.1 and 6.5 square inches. This procedure repeats until enough individual are generated to fill the initial population. The genetic algorithm then searches for a structure that satisfies design constraints and minimizes the objective function described below. For simplicity, only the most important design constraints, which are constraints on stress in the truss members and deflection of the truss, are used.

Here and are the allowed and the actual stress for each truss member and and are the allowed and actual vertical deflections, at a predetermined truss node. and are penalty weights. Excessive stresses, excessive nodal displacements, and underutilization of material are penalized. Generated trusses that disobey hard constraints on nodal displacements and member stresses are more heavily penalized than those that satisfy these constraints. For example, overstressed members are penalized more than understressed members. Thus, takes a larger value if as does if . p1 and p2 will take a smaller value if or . The smaller values penalize the truss for wasted material. Ideally, an optimal solution will be of minimum weight with and , since maximum utilization of material implies that all members are stressed to the design limits and the truss has just enough stiffness to satisfy the deflection requirement. However, it has been shown that optimal solutions may not always exist using the full stress design criterion [Save and Prager, 1985].

  
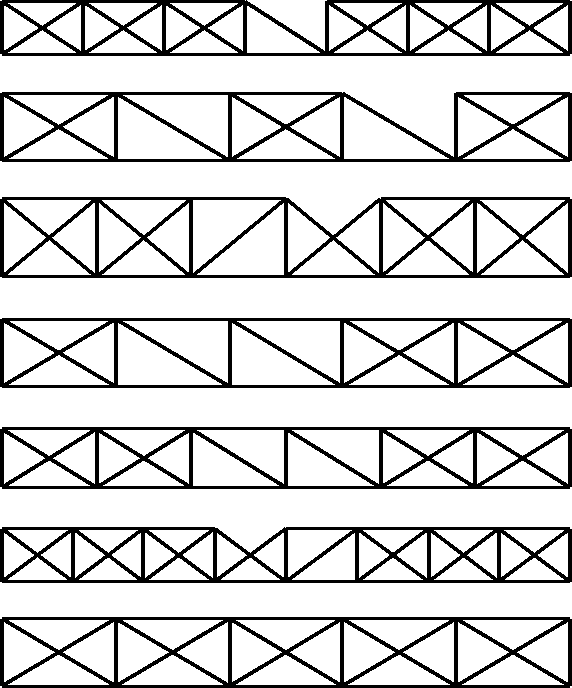
Figure 4: Trusses produced by the initiation procedure.

Figure 4 presents some of the trusses produced at initiation. The objective function returns a fitness value that is minimized to drive the genetic search in the direction of feasible, minimal weight solutions.

Representation and the Effect of Genetic Operators

Unlike traditional genetic algorithm representations that emphasize bit strings, we use a mixed representation, employing bit strings as well as more complex structures. This makes it easier to add heuristic constraints to the problem and reduces the size of the search space. Panel sizes are not subject to crossover and are fixed for an individual limiting exploration of this parameter to within the space spanned by the initial population.

Selection in genetic algorithms concentrates search in a promising area and is the exploitation operator. We discuss selection in the next section.

We want the crossover and mutation operators to generate new structures and guide exploration of the search space of possible truss structures. Starting with a statically determinate truss (triangularized), we need to be able to change the topology, geometry, and member cross sections in order to explore the space.

Exploring member cross sections and truss depths is fairly straightforward. We store these parameters as binary strings. Crossover and mutation as defined in the section on genetic algorithms suffice to explore the space of possible cross sections and truss depths.

Although changing the depth of nodes explores some of the topological space, we do not change the geometry. We define new crossover and mutation operators which are not simple bit string exchanges but in keeping with the spirit of genetic algorithms, have the effect of exchanging information.

Since crossover in genetic algorithms combines good substructures to improve solutions, we implement structural crossover by randomly selecting a contiguous set of nodes on the top chord and exchanging them as well as the members connected to them. Figure 5 depicts the result of crossing over the two structures on the bottom. The nodes to be crossed over are labeled [1,4] and [1,5] (shaded) and exchanging these nodes results in the structures labeled ``child 1'' and ``child 2.'' Intuitively, ``child 1'' is a copy of ``parent 1'' except for the nodes that came from ``parent 2'' and vice versa.

  
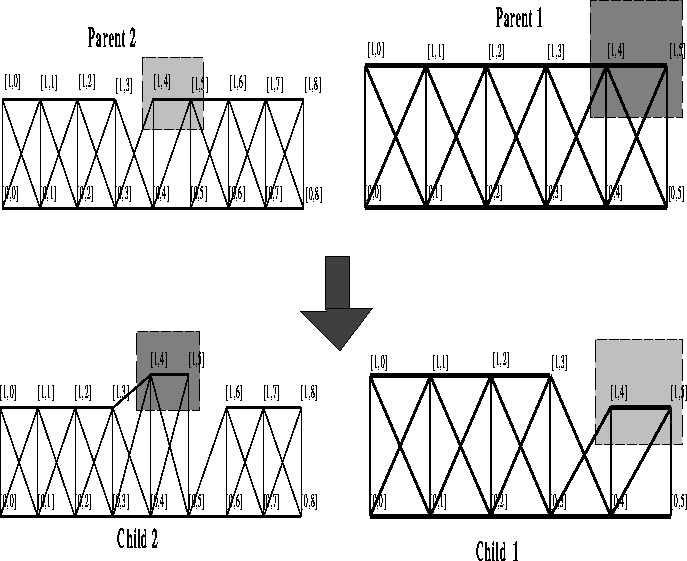
Figure 5: Structural crossover of trusses. Nodes [1,4] and [1,5] are exchanged.

Thus, structural crossover has the effect of changing both the topology and geometry of trusses in the population. Since member cross sectional areas are exchanged along with the members attached to a node, the cross sectional areas change in this way as well. Structural mutation adds and deletes non-randomly chosen members and nodes, and randomly perturbs member cross sectional areas. We encode engineering heuristics in the structural mutation operator by biasing it toward removing members with low stresses and adding members to nodes with large displacements. The probability of a member's removal due to structural mutation is inversely proportional to the stress on that member while the probability of a member being added to a node is directly proportional to the displacement. Top chord nodes can be removed through random mutation although there is no provision for adding nodes.

Recombination of this kind may generate trusses that are statically indeterminate (not triangularized). Every offspring is therefore checked and, if needed, additional members are added to brace and triangularize the truss.