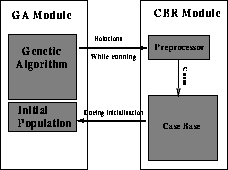
Figure 1: Conceptual view of our system
Genetic algorithms provide an efficient tool for searching large, poorly
understood spaces often encountered in function optimization and machine
learning [Holland, 1975]. The probabilistic nature of GA search allows
GAs to be successfully applied to a variety of NP-hard problems
[Goldberg, 1989, Powell et al., 1989, Caldwell and Johnston, 1991]. The population-based, emergent nature
of computation in GAs lends them a degree of robustness and flexibility
that is often unobtainable using other approaches.
A genetic algorithm explores a subset of the search space during a problem solving attempt and its population serves as an implicit memory guiding the search. Every individual generated during a search defines a point in the search space and the individual's evaluation provides a fitness. This information when stored, organized, and analyzed can be used to explain the solution, that is, tell which parts of the genotype are important, and allow a sensitivity analysis [Louis et al., 1993]. However, this information is usually discarded at the end of a GA's run and the resources spent in gaining this information are wasted. If we store this information (explicit memory) and use it in a subsequent problem solving attempt on a related problem we can tune the GA to a particular space and thus increase performance in this space.
One early attempt at reuse can be found in Ackley's work with SIGH [Ackley, 1987]. Ackley periodically restarts a search in an attempt to avoid local optima and increase the quality of solutions. Eshelman's CHC algorithm, a genetic algorithm with elitist selection and cataclysmic mutation, also restarts search when the population diversity drops below a threshold [Eshelman, 1991]. Both approaches only attack a single problem not a related set of problems. Ramsey and Grefenstette come closest to our approach and use previously stored solutions to initialize the genetic algorithm's initial population and thus increase a genetic algorithm's performance in an environment that periodically changes with time [Ramsey and Grefensttete, 1993]. They report encouraging results in such environments (better performance). Our work however, tackles sets of similar problems and addresses the issues of which and how many cases to inject into the population. To our knowledge, the earliest work in combining genetic algorithms and case-based reasoning was done by Louis, McGraw, and Wyckoff who used case-based reasoning principles to explain solutions found by genetic algorithm search [Louis et al., 1993].
Figure 1 shows a conceptual view of a simple version of our system. There are two basic modules, the search module and the CBR module. The search module in this paper consists of a genetic algorithm and the CBR module for this work only contains a few cases relevant to the problem we are going to solve. When confronted with a problem, the CBR module looks in its case base for similar problems and their associated solutions. If any similar problems are found their solutions are injected into the initial population (a small percentage of the population is initialized this way) of the genetic (or other search) algorithm and the GA searches from this population.

Figure 1: Conceptual view of our system
The case-base does what it is best at -- memory organization; the genetic algorithm handles what it is best at -- adaptation. The resulting combination takes advantage of both paradigms; the genetic algorithm component delivers robustness and adaptive learning while the case-based component speeds up the system.
The genetic algorithm also provides a ready-made case generating
mechanism as each individual generated during a GA search can be thought
of as part of a case. However, even a population size of a 100 run for
a 100 generations can generate up to ![]() cases
leading to problems with storage and indexing. CBR systems usually have
difficult in finding enough cases; our problem is the opposite. We need
to sift through a large number of cases to find potential seeds for the
initial population. CBR systems often include principled mechanisms for
generalization and abstraction of cases because it may be impractical to
store all prior experience in detail. For our system, generalized
individuals correspond to schemas (subsets of the search space) and can
be stored as cases. This is described in [Louis et al., 1993]. Since genetic
algorithms should be used in poorly-understood domains, one side-effect
of this approach is that the generalizations and abstractions may in
fact induce a useful domain model.
cases
leading to problems with storage and indexing. CBR systems usually have
difficult in finding enough cases; our problem is the opposite. We need
to sift through a large number of cases to find potential seeds for the
initial population. CBR systems often include principled mechanisms for
generalization and abstraction of cases because it may be impractical to
store all prior experience in detail. For our system, generalized
individuals correspond to schemas (subsets of the search space) and can
be stored as cases. This is described in [Louis et al., 1993]. Since genetic
algorithms should be used in poorly-understood domains, one side-effect
of this approach is that the generalizations and abstractions may in
fact induce a useful domain model.
There are at least three points of view to consider when combining genetic algorithms and case-based reasoning.
Our results on the open shop scheduling (OSSP) and re-scheduling problems (OSRP) establish the feasibility of this approach and shed light on some of the issues above and raise others to explore. In the next section, we describe a simple system to test the feasibility of combining genetic algorithms and case-based reasoning on OSSP and OSRP problems.