Methodology and Results

In our experiments, a genetic algorithm finds and saves solutions to an open shop scheduling problem , the problem is changed slightly to , and appropriate solutions to are injected into the initial population of the genetic algorithm that is trying to solve the new problem . If the cases from contain good building blocks or partial solutions, the genetic algorithm can use these building blocks or schemas and quickly approach the solution to . The results show that compared to a genetic algorithm that starts from scratch (from a randomly initialized population), the genetic algorithm with injected solutions very quickly finds good solutions to and that the quality of solutions after convergence is usually better.

Open Shop Scheduling and Re-Scheduling

The open-shop scheduling problem is an important practical scheduling problem, but is known to be very hard to solve in a reasonable amount of time. Re-scheduling is also an important aspect of the problem in the real world. It involves modifying a schedule in the process of execution in order to take account of a changing environment. In the general open-shop scheduling problem, there are j jobs and m machines. Each job contains a set of tasks which must be done on a different machine for a different amount of time, with no a-priori ordering on the tasks within a job. The problem is to minimize the makespan, the total time between the beginning of the first task till the end of the last task. A valid schedule is a schedule of job sequences on each machine such that a machine is not processing two different tasks at the same time, and different tasks of the same job are not simultaneously being processed on different machines. We must take into account both resources and time constraints with the aim of finding a valid schedule with a minimum makespan. The OSSP differs from the job-shop scheduling problem in that there is no a-priori ordering on the tasks within a job. This leads to an extremely large search space. For example on a OSSP, there are 25! different task orderings which is approximately equal to different valid schedules.

In open-shop re-scheduling (OSRP), we need to be able to handle changing conditions on the shop floor. For example, jobs may be canceled, machines may fail, or we may run low on inventory. If the work has not yet begun on the current schedule, then a simple way of re-scheduling is to rerun the GA for this scheduling problem in the changed environment. We need quick and efficient methods of re-scheduling to tackle the problems of frequently changing environments. In this paper we handle the case of a machine breaking down and being replaced with a new, faster machine. is the problem with the old machine while is the problem with the new machine, where the processing times of all tasks on the new machine have been decreased by 10 time units; note that we have made sure that is similar to . We use individuals from a GA's run on as cases for the re-scheduling problem, . After using a variety of criteria to pick individuals for cases and to choose how many individuals to inject into the initial population of size 200 run for 300 generations, we obtained good performance under the following conditions (More details on the encoding and genetic operators are available in  [Xu and Louis, 1996]).

1. We inject only 8 cases into the initial population. Injecting between and of the population usually produced good results across the set of population sizes that we tried. Injecting a small percentage of the population establishes a good balance between exploration and exploitation of the search space. The injected individuals, if chosen well, represent good schema and help the GA quickly find promising solutions.
2. The individuals chosen as cases were:
   • The best individuals in the first and the last generations (Since we used a kind of elitist selection, the best individual in the last generation was the best ever).
   • Six good individuals in the generations between the first and last. For example, if we ran for 300 generations, then we pick the best individuals in generations which are a multiple of 300/6 = 50 .

We mutated these six individuals picked from intermediate generations and inject all eight individuals into the initial population of the GA for the OSRP. Figure 2 compares the average performance of a genetic algorithm initialized with these cases with a randomly initialized GA on two different OSRP problems. We call the the GA that uses cases a Case Initialized Genetic AlgoRithm or CIGAR, and the Randomly Initialized GA, RIGA in the rest of this paper. The graphs in this section display the best makespan averaged over 10 runs with different random seeds.

  
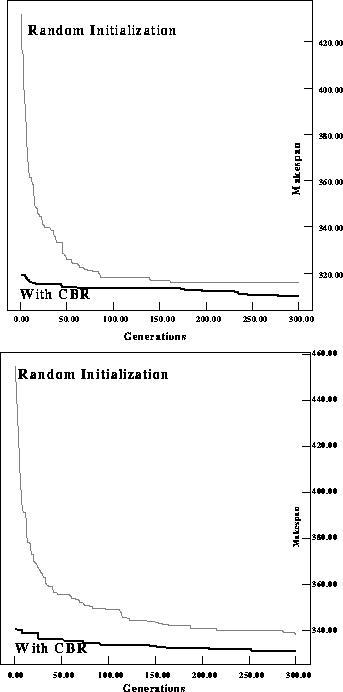
Figure 2: Comparing performance of a RIGA with a CIGAR for 5x5 OSRP problems.

We can see that the CIGAR starts with a much lower (better) initial best makespan and that even after 300 generations CIGAR solutions are better than solutions from a randomly initialized GA. Table 1 compares starting and ending makespans for eight different OSSP benchmark problems. The last column specifies the machine that was changed (picked randomly). Notice that CIGAR does comparatively well in early generations and provides good schedules more quickly than the randomly initialized GA.

  
Table 1: Performance comparison of average makespan on 5x5 OSRP problems

We get similar results on a set of five OSRP benchmark problems. Figure 3 displays average best makespans over ten runs with different random seeds on two of the problems. We increase the population size to 300 and run for 400 generations on the problems. Once again

  
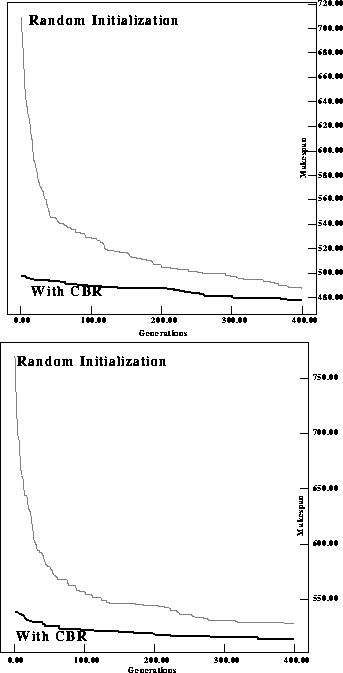
Figure 3: Comparing performance of a RIGA with a CIGAR for 7x7 OSRP problems

the CIGAR does better, especially in early generations.