


Next: Genetic Algorithms
Up: Robust Stability Analysis of
Previous: Introduction
Consider a linear time invariant discrete-time system. The stability of the
system can be determined by examining its characteristic equation. The
characteristic equation may be written as:
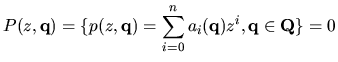 |
|
|
(1) |
where
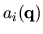 ,
i =0, 1, ..., n are functions of the uncertain
plant parameter vector
,
i =0, 1, ..., n are functions of the uncertain
plant parameter vector 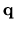 ,
and
,
and
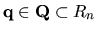 .
The coefficients ai may be interval, affine, multilinear
or even exponentially dependent on the uncertain plant
parameter vector
.
The coefficients ai may be interval, affine, multilinear
or even exponentially dependent on the uncertain plant
parameter vector 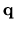 .
When the coefficients are nonlinear, traditional
methods fail, and overbounding or gridding are our only options.
Unfortunately, overbounding gives conservative stability results while gridding
is only feasible for a small number of parameters.
.
When the coefficients are nonlinear, traditional
methods fail, and overbounding or gridding are our only options.
Unfortunately, overbounding gives conservative stability results while gridding
is only feasible for a small number of parameters.
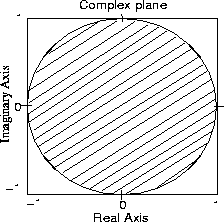
The stability boundary for Equation (1) is |z| = 1. The stability test is to
determine if there exists a system pole outside the unit circle. Using the
mapping
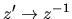 ,
the instability region becomes the
closed unit disc
,
the instability region becomes the
closed unit disc 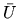 ,
and therefore, system instability testing reduces
to searching for a pole inside or on the unit circle (see Figure 1).
,
and therefore, system instability testing reduces
to searching for a pole inside or on the unit circle (see Figure 1).
If the polynomial coefficients are continuous functions of the uncertain
parameters and no degree dropping occurs,
the system instability test can be simplified to searching for a root on the
unit circle and the mapping
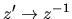 need not be used.
This follows from the well known boundary crossing theorem [10].
need not be used.
This follows from the well known boundary crossing theorem [10].
Figure:
Roots of
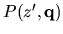 in the unit circle
in the unit circle
 |
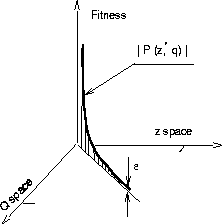
Searching for a root inside or on the unit circle can be formulated as
minimizing the cost function
Figure 2:
Minimization of a cost function
 |
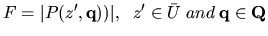 |
|
|
(2) |
with tolerance 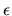 as shown in Figure 2 and where
as shown in Figure 2 and where 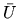 denotes the closed unit disc and
denotes the closed unit disc and 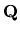 is the set of feasible parameter
vectors. The robust stability problem can now be stated as follows: Given a
family of characteristic functions P associated with uncertain physical
parameters
is the set of feasible parameter
vectors. The robust stability problem can now be stated as follows: Given a
family of characteristic functions P associated with uncertain physical
parameters 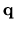 ,
search the space
,
search the space
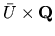 for a minimal
value of
for a minimal
value of
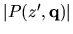 ,
,
 and
and 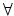
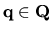 .
If
.
If 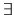 a "zero" of
a "zero" of
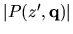 ,
then the system is unstable. If the polynomial is continuous and no degree
dropping occurs, we search for the roots on the unit circle. If
,
then the system is unstable. If the polynomial is continuous and no degree
dropping occurs, we search for the roots on the unit circle. If
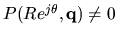 ,
,
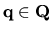 ,
,
![$\theta \in
[0, \pi]$](img20.gif) and R = 1, then further search inside the unit circle will be
necessary.
Thus there are two main possibilities:
and R = 1, then further search inside the unit circle will be
necessary.
Thus there are two main possibilities:
- 1.
- If we find a ``zero'' on or inside the unit circle, we have sufficient evidence to conclude that the system is unstable
- 2.
- Otherwise, if we do not find a ``zero'' there are two further
possibilities.
- (a)
- The system is unstable but the genetic algorithm cannot find
a ``zero,'' or
- (b)
- The system is stable
We cannot distinguish between 2a and 2b and thus our approach can
only provide a sufficient condition for instability, not a necessary
condition. Specifically, not finding a ``zero'' of the polynomial does not
provide any information about system stability.
A key issue that arises in this approach is the extremely large search
space. In such a large search space, exhaustive search methods take
unacceptably long while robust search algorithms provide a promising
alternative. Genetic algorithms were designed to robustly and efficiently
search large, nonlinear search spaces where traditional optimization techniques
are not feasible. GAs are particularly attractive because they do not require
the coefficients of the characteristic polynomial to be linear and we thus
choose to use GAs as the search method for this paper.



Next: Genetic Algorithms
Up: Robust Stability Analysis of
Previous: Introduction
Sushil Louis
1998-10-23
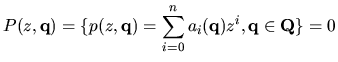
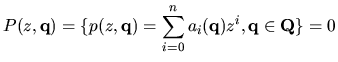
![]() ,
the instability region becomes the
closed unit disc
,
the instability region becomes the
closed unit disc ![]() ,
and therefore, system instability testing reduces
to searching for a pole inside or on the unit circle (see Figure 1).
,
and therefore, system instability testing reduces
to searching for a pole inside or on the unit circle (see Figure 1).
![]() need not be used.
This follows from the well known boundary crossing theorem [10].
need not be used.
This follows from the well known boundary crossing theorem [10].