 |
GAs are stochastic, parallel search algorithms based on the mechanics of natural selection and the process of evolution [24,12]. GAs were designed to efficiently search large, nonlinear spaces where expert knowledge is lacking or difficult to encode and where traditional optimization techniques fail. GAs perform a multi-directional search by maintaining a population of potential solutions usually encoded as bit strings and encourage information formation and exchange between these solutions. A population is modified by the probabilistic application of the genetic operators from one generation to the next. Whenever some individuals in the population exhibit better than average performance, the genetic features of these individuals will be copied with high probability to the next generation.
Evaluation of each string which encodes a candidate solution is based on a
fitness function that is problem dependent. Selection is done on the basis of
relative fitness and it probabilistically culls solutions from the population
that have relatively low fitness. Recombination consists of mutation and
crossover. Mutation insures against the permanent loss of genetic material
during the selection process and with low probability flips a bit in the
genotype. Crossover is a structured yet stochastic operator that allows
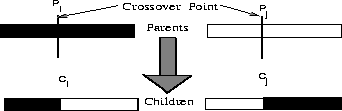
information exchange between candidate solutions. Figure 3 shows that
one point crossover is implemented by choosing a random point in the selected
pair of strings and exchanging complementary substrings defined by the chosen
point.