Next: Representation
Up: Robust Stability Analysis of
Previous: Genetic Algorithms
In the general case, the closed-loop characteristic polynomials is defined in
parametric form as
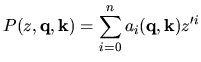 |
|
|
(3) |
The controller parameter vector 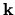 and the operating domain Q are
given. In such a polynomial family, the coefficient
and the operating domain Q are
given. In such a polynomial family, the coefficient
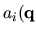 ,
,
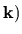 include any continuous nonlinear functions, in which we are particularly
interested in coefficients with nonlinear dependency. The roots of this
polynomial are complex and equal to
include any continuous nonlinear functions, in which we are particularly
interested in coefficients with nonlinear dependency. The roots of this
polynomial are complex and equal to
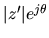 and the range of
and the range of
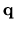 is defined by its pre-specified minimum and maximum values
is defined by its pre-specified minimum and maximum values
![$[{\bf
q}^-, {\bf q}^+]$](img27.gif) .
The objective of the genetic algorithm is to find:
.
The objective of the genetic algorithm is to find:
![$\displaystyle f(z, q) = Min[\vert P(z^{\prime}, {\bf Q})\vert],\:\:{q \in {\bf Q}, \: z \in \bar{U}}$](img28.gif) |
|
|
(4) |
where
We exploit the fact that for real coefficients, roots are complex conjugate
pairs or real. Hence, the search space can be restricted to the
upper half of the unit circle shown in Figure 1.



Next: Representation
Up: Robust Stability Analysis of
Previous: Genetic Algorithms
Sushil Louis
1998-10-23