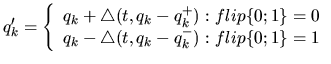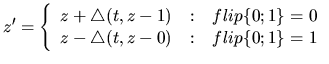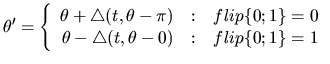Next: Tuning Genetic Algorithms
Up: GA Encoding for Robust
Previous: GA Encoding for Robust
We use a small margin of tolerance 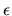 to represent a true numeric
zero.
to represent a true numeric
zero. 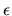 can be the computer's floating-point precision, or double
precision, since high precision is required in our problem. Additionally, the
uncertain polynomial in real applications may contain numerous parameters. In
such uncertain parameter optimization problems, a long bit string is required
in order to extend the precision and represent the entire range of each
parameter. Thus the binary chromosome representation traditionally used in GAs
shows some deficiencies since a long chromosome usually results in poor
performance for GAs.
can be the computer's floating-point precision, or double
precision, since high precision is required in our problem. Additionally, the
uncertain polynomial in real applications may contain numerous parameters. In
such uncertain parameter optimization problems, a long bit string is required
in order to extend the precision and represent the entire range of each
parameter. Thus the binary chromosome representation traditionally used in GAs
shows some deficiencies since a long chromosome usually results in poor
performance for GAs.
In order to overcome the drawback of the binary representation, we coded the GA
chromosome as a vector of real numbers with double precision. Each parameter
qi, i=1,...,n, is initialized within the pre-specified domain
[qi-,
qi+]. The magnitude of the root
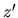 is initially selected to be
within [0, 1], while the angle
is initially selected to be
within [0, 1], while the angle 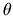 is in the interval
is in the interval ![$[0,
\pi]$](img34.gif) .
Compared with binary representation, real numbers are better capable of
representing our desired domain. The precision only depends on the machine we
use and the accuracy depends on the user's requirements. We define the
chromosome for the uncertain polynomial
.
Compared with binary representation, real numbers are better capable of
representing our desired domain. The precision only depends on the machine we
use and the accuracy depends on the user's requirements. We define the
chromosome for the uncertain polynomial
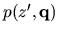 as:
as:
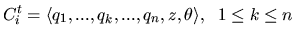 |
|
|
(5) |
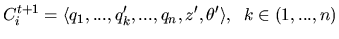 |
|
|
(6) |
where Cit is the chromosome of population i in tth generation.
Cit+1 is a new chromosome for the next generation after genetic
selection. The
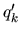 ,
,
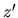 and
and
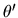 in
Cit+1 satisfy
in
Cit+1 satisfy
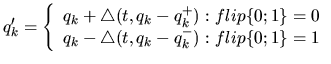 |
|
|
(7) |
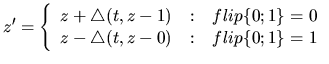 |
|
|
(8) |
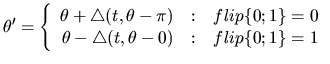 |
|
|
(9) |



Next: Tuning Genetic Algorithms
Up: GA Encoding for Robust
Previous: GA Encoding for Robust
Sushil Louis
1998-10-23
![]() to represent a true numeric
zero.
to represent a true numeric
zero. ![]() can be the computer's floating-point precision, or double
precision, since high precision is required in our problem. Additionally, the
uncertain polynomial in real applications may contain numerous parameters. In
such uncertain parameter optimization problems, a long bit string is required
in order to extend the precision and represent the entire range of each
parameter. Thus the binary chromosome representation traditionally used in GAs
shows some deficiencies since a long chromosome usually results in poor
performance for GAs.
can be the computer's floating-point precision, or double
precision, since high precision is required in our problem. Additionally, the
uncertain polynomial in real applications may contain numerous parameters. In
such uncertain parameter optimization problems, a long bit string is required
in order to extend the precision and represent the entire range of each
parameter. Thus the binary chromosome representation traditionally used in GAs
shows some deficiencies since a long chromosome usually results in poor
performance for GAs.
![]() is initially selected to be
within [0, 1], while the angle
is initially selected to be
within [0, 1], while the angle ![]() is in the interval
is in the interval ![]() .
Compared with binary representation, real numbers are better capable of
representing our desired domain. The precision only depends on the machine we
use and the accuracy depends on the user's requirements. We define the
chromosome for the uncertain polynomial
.
Compared with binary representation, real numbers are better capable of
representing our desired domain. The precision only depends on the machine we
use and the accuracy depends on the user's requirements. We define the
chromosome for the uncertain polynomial
![]() as:
as: