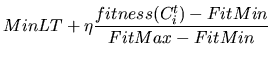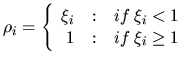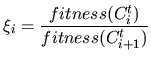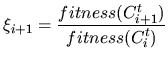Next: Results
Up: GA Encoding for Robust
Previous: Representation
We assume that the polynomial
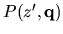 contains nonlinear
coefficients, and may therefore have numerous finite local
extrema. To enhance the GAs ability to efficiently find a desired global
minimum hidden among many local extrema, a good balance between
exploration and exploitation is necessary, as shown in Figure 4.
contains nonlinear
coefficients, and may therefore have numerous finite local
extrema. To enhance the GAs ability to efficiently find a desired global
minimum hidden among many local extrema, a good balance between
exploration and exploitation is necessary, as shown in Figure 4.
Figure 4:
Exploration and exploitation
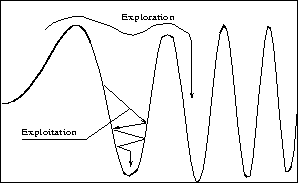 |
Our strategy is to give GAs a richer population and more exploration to avoid
unfavorable local minima in early stages. Later, we gradually reduce the number
of such minima qualifying for frequent visits. The attention finally shifts
more to smaller refinements in the quality of solution.
Instead of constant population size, we introduce a varying population size
schedule by utilizing information about the individual fitness. This has also
been investigated in [25,26,27,22].
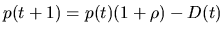 |
|
|
(10) |
where p(t+1) is the population size for next generation; p(t) is the
size of current population; 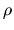 is the reproduction ratio and D(t) is
the number of expired individuals. The individual lifetime can be
determined by
is the reproduction ratio and D(t) is
the number of expired individuals. The individual lifetime can be
determined by
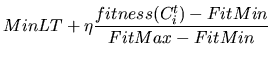 |
|
|
(11) |
where FitMax and FitMin are maximal and minimal fitness values found until
the current generation, respectively. MinLT is minimal allowable lifetime and
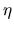 is a constant which can be set to greater than 1. Although varying
the population size introduces additional complexity in out implementation, our
tests indicate that the output quality improves significantly and the number of
generations needed for searching a desired global optimum decreases compared
with the canonical genetic algorithm.
is a constant which can be set to greater than 1. Although varying
the population size introduces additional complexity in out implementation, our
tests indicate that the output quality improves significantly and the number of
generations needed for searching a desired global optimum decreases compared
with the canonical genetic algorithm.
The mutation schedule known as non-uniform mutation
can be stated as follows [27]:
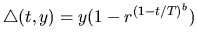 |
|
|
(12) |
where r is a random number in [0,1], and b is a system parameter
determining the degree of nonuniformity, and y equals to
(qk - qk+) or
(qk - qk-) for uncertain parameters, (z-1) or (z-0) for the absolute
value of the root and
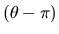 or
or
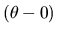 for the angle of the
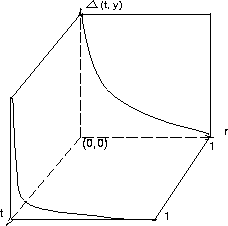
root. Figure 5 shows the behavior of mutation operators. The
property of this mutation schedule is to help the GA wander freely among local
minima at early stages. The attention of mutation then shifts to smaller
refinements in the solution at later stages when we are in the vicinity of a
possible global optimum. Based on our tests results, a large mutation
rate is suggested.
for the angle of the
root. Figure 5 shows the behavior of mutation operators. The
property of this mutation schedule is to help the GA wander freely among local
minima at early stages. The attention of mutation then shifts to smaller
refinements in the solution at later stages when we are in the vicinity of a
possible global optimum. Based on our tests results, a large mutation
rate is suggested.
Figure 5:
The behavior of our mutation operator
 |
We assume Cit and Ci+1t to be two individuals of population
p(t) at generation t. Their offspring for the next generation t+1are generated by linearly combining these two individuals. The resulting
offspring are generated by the rules
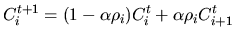 |
|
|
(13) |
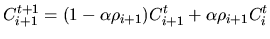 |
|
|
(14) |
where 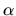 is the value of the random variable distributed on
[0,1].
is the value of the random variable distributed on
[0,1]. 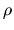 is a bias factor that specifies how much
additional information is taken from the dominating individual (higher fitness)
in the current stage. The new offspring attempt to inherit the better genes
from each of their parent. Assuming maximization
problems with a non-negative fitness function,
is a bias factor that specifies how much
additional information is taken from the dominating individual (higher fitness)
in the current stage. The new offspring attempt to inherit the better genes
from each of their parent. Assuming maximization
problems with a non-negative fitness function, 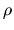 can then be
determined from the following equations.
can then be
determined from the following equations.
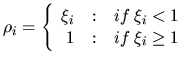 |
|
|
(15) |
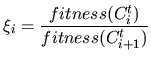 |
|
|
(16) |
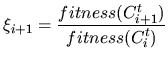 |
|
|
(17) |
Implementing these two equations does not raise the genetic algorithm's
computational complexity and, based on our numerical tests, the performance of
our modified genetic algorithm is significantly better than that of a canonical
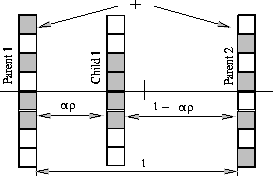
genetic algorithm. Figure 6 illustrates this crossover
operator. When parent 1 shows better fitness than parent 2, child 1 is
allowed to copy additional information from parent 1. As a result, the
chromosome of child 1 retains more similarity with parent 1.
Figure 6:
The mechanism of crossover operator
 |



Next: Results
Up: GA Encoding for Robust
Previous: Representation
Sushil Louis
1998-10-23
![]() contains nonlinear
coefficients, and may therefore have numerous finite local
extrema. To enhance the GAs ability to efficiently find a desired global
minimum hidden among many local extrema, a good balance between
exploration and exploitation is necessary, as shown in Figure 4.
contains nonlinear
coefficients, and may therefore have numerous finite local
extrema. To enhance the GAs ability to efficiently find a desired global
minimum hidden among many local extrema, a good balance between
exploration and exploitation is necessary, as shown in Figure 4.