[The great supercomputer, asked what is the answer to] the great problem of life, the universe and everything [replied, after many years of computation] 42.- Douglas Adams, The Hitch-hiker's Guide to the Galaxy
As illustrated in the last chapter, solutions generated by genetic algorithms may be difficult to understand. There are two main reasons for this:
During the course of a GA's search through the underlying space for a design, it implicitly extracts and uses information about the space. The kind of information extracted and used by a genetic algorithm depends on the specific operators used and is indicated by the schema theorem and building block hypothesis. However, this knowledge is never made explicit and is discarded at the end of a GA's run. This thesis describes a system that uses tools developed for case-based reasoning and genetic algorithm theory to identify, extract, and organize this information. The organized knowledge can be used to learn about the domain, to explain how a solution evolved, to discover its building blocks, to justify why it works, and to tune the GA in various ways.
The chapter starts with a short introduction to case-based reasoning, describes the system, and clarifies the results using examples from circuit design and function optimization.
Case-based reasoning (CBR) is based on the idea that reasoning and explanation can best be done with reference to prior experience, stored in memory as cases [Bareiss, 1991, Riesbeck and Schank, 1989]. When confronted with a problem to solve, a case-based reasoner extracts the most similar case in memory and uses information from the retrieved case and any available domain information to tackle the current problem. The strategy is first to collect and index a large and varied collection of examples, and then, when presented with a new situation, to fetch and possibly manipulate the stored example that most closely resembles the new situation. Each stored case may be considered a previously evaluated data point, the nature and location of which is problem-dependent. If the distance metrics have been well designed and the case base includes sufficient variety, retrieved cases reveal useful conclusions from previous analysis. Because it may be impractical to store all prior experience in detail, CBR systems often include principled mechanisms for generalization and abstraction of cases. Note that except when comparing distinct cases, a CBR system need not include any notion of an underlying model of the domain of application, and that even during comparison one can make do without much of one. One side-effect of this approach is that the generalizations and abstractions may in fact induce a useful domain model. This chapter uses the basic tenet of CBR -- the idea of organizing information based on ``similarity'' -- to help explain the solutions generated by a genetic algorithm.
GA theory tells us little about the actual path a given GA will take through the space on its way to an answer. Because of the stochastic nature of GA operators, a solution's optimality is not guaranteed and its building blocks are unknown.
Information about the building blocks is implicit in the processing done by a GA but is not documented explicitly or available to the user. Keeping track of historical regularities and trends is the key to acquiring the knowledge needed to explain what sort of solution evolved, why it works, and where it came from. Discovering building blocks by explicitly keeping track of the GA's search trajectory allows principled partitioning of the search space. Empirical regularities can be formalized and possibly put to use. The individuals in a GA's population act as a primitive memory for the GA. Genetic operators manipulate the population, usually leading the GA away from unpromising areas of the search space and towards promising ones, without the GA having to explicitly remember its trail through the search space. Genetic algorithms trade the use of explicit memory for speed and simplicity. This chapter uses the methods and tools developed for case-based reasoning to extract, store, index and (later) retrieve information generated by a GA. Individuals created by the GA provide a set of initial cases from which a well-structured case-base can be constructed.
Defining an appropriate index or measure of similarity among the cases is one of the first tasks in creating a case-base. The building block hypothesis implies that syntactically similar (short and low-order), high-performance individuals bias genetic search. Since genetic algorithms process syntactic similarity and fitness as stated in the building block hypothesis, this thesis uses fitness and genotype (the encoded design) as metrics for indexing the case-base. These measures provide the key to indexing the cases and conveniently solve one of the hardest of CBR problems.
CBR's model of information organization is applied to GAs as an analysis tool in order to track the history of a search. The system (described below) creates a case for each individual that the GA has evaluated. These cases are indexed on syntactic similarity and fitness. When properly formed and analyzed, this case-base can contribute to the understanding of how a solution was reached, why a solution works, and what the search space looks like. At the interruption (or termination) of a GA run, the case-base allows the interpretation and subsequent modification of discovered solutions.
In addition, during the course of a run, as the system digests more information, it can generate hypotheses about the space. These hypotheses, which take the form of new individuals injected into the GA's population, can be tracked and evaluated, testing the validity of the hypotheses. Given proper hypothesis formation, the system can guide evolution more directly towards convergence. False hypotheses may provide evidence of deception in the current search space.
The system is made up of a genetic algorithm which runs in tandem with an
analysis module (see figure 
).
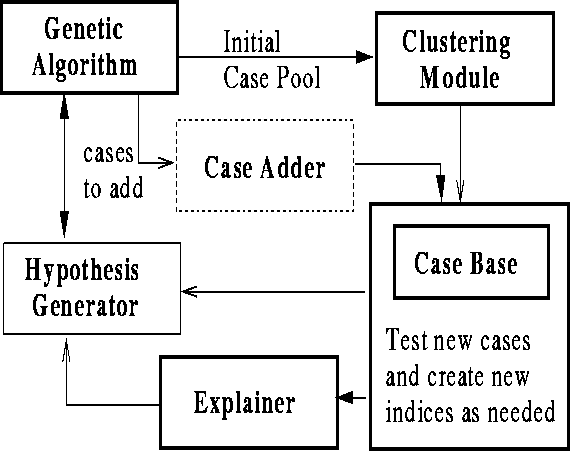
Figure: Schematic diagram of the system
The genetic algorithm records data for each individual in the population as it is created and evaluated. This data includes a fitness measure, the genotype, and chronological data, as well as some information on the individual's parents. This collection of data is the initial case data. Though normally discarded by the time an individual is replaced, all of the case data collected is usually contained in the genetic algorithm's population at some point and is easy to extract.
After a sufficient number of individuals have been created over a number of
generations, the initial case data is sent to a clustering program. A
hierarchical clustering program clusters the individuals based on both the
fitness and the alleles of the genotype. This clustering constructs a binary
tree in which each leaf includes the data of a specific individual. The binary
tree structure provides an index for the initial case-base.
Figure shows a small part of one such tree. The numbers at
the leaves of the tree correspond to the case number (an identification number)
of an individual created by the GA. Internal nodes are denoted with a ``*''.
An abstract case is computed for each internal node based on the information
contained in the leaves and nodes beneath it. The final case-base includes: 1)
cases corresponding directly to GA individuals (at the leaves) and 2) more
abstract cases made up of information generalized from the leaves.
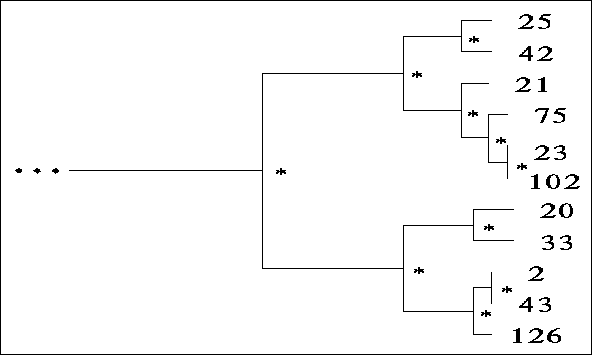
Figure: A small subsection of a typical binary tree
created by the clustering algorithm. Individuals are represented by
the numbers at the leaves. Internal nodes where abstract cases go are
denoted with a ``*''. The binary tree provides an index for the case-base.
Although a number of clustering techniques and clustering sets are possible
(for example, fitness and genotype data versus fitness alone), standard
hierarchical clustering on fitness and genotype produces a coherent initial
index for the case-base. The fact that fitness and genotype matter the most is
predicted by the building block hypothesis and borne out experimentally. After
an index has been created, several easy computations are recursively performed
to flesh out the abstract cases (these computations are explained in
Section ).
The hypothesis generator runs in tandem with the GA. Using information from the the case-base, it engineers individuals for injection into the population. Information about the measured performance of such individuals relative to the remainder of the population can also be fed back into the hypothesis module for analysis. The success or failure of generated hypotheses can be used in decisions regarding the validity of the current case-base.
At the end of a run, a well-developed case-base can be used to explain how the GA came up with its answer, and why that answer is strong. The system can explain something about where the winning answer came from, which of its building blocks are the strongest, and which the weakest. This sort of data allows any future search of the space to be fine-tuned. It also allows post facto analysis. Much of the knowledge that is usually discarded by a GA is made available in processed form for future manipulation.
Clustering the first few hundred individuals using genotype and fitness values produces a case-base. As explained above, clustering determines the indexing scheme of the case-base. All abstract cases, which are indexed at the internal nodes of the tree, must be recursively computed from the leaves up. Although much of the initial case data saved during the GA run is not used by the clustering algorithm, it is added to the cases in the case-base.
Cases include the following information:
Using the information in the case-base, the system produces a report regarding the GA run so far. Using fitness as a metric, computing the top-ranked or bottom-ranked n cases is easy, as is finding the top-ranked or bottom-ranked n case schemas. These schemas can be combined to make new schemas by applying standard schema creation rules. For example, the two schemas **110**10 and **100***0 combine to the new schema **1*0***0. The resulting schemas show (among other things) which alleles are important in the genotype and which ones are not. Since order, longevity, and weight information is available, it is straightforward to find the top few cases with given sets of these characteristics.
It is also useful to calculate not only the schema that includes the subset of leaf cases, but one that records in a more democratic fashion the relative frequency of allele settings for the positions which are not absolutely fixed. Since the normal schema-producing rules result in a ``*'' wherever there is disagreement about an allele among leaves, schemas near the top of the tree tend to be filled with ``*''s. To avoid this information loss, the system generates an additive schema by computing the bitwise sum of the genotypes associated with the leaves below.
An elected schema can be computed by dividing the additive schema by the
weight and squashing the results to 0, 1, or ``*'' using thresholds that can
be changed. Elected schema information provides a more informative way of
looking at upper-level schemas. Elected schemas play a large role in
hypothesis generation, discussed in section .
A schema actually describes a convex hull for the leaves from which it was computed. That is, it describes a portion of the space within which the unaltered leaves fit. Since the normal schema-producing rules result in top-level schemas with a large number of ``*''s and the hull tends to span too large a portion of the entire space, it is preferable to describe a smaller hull, one for which the average hamming distance from an actual leaf to the hull surface is less than some predetermined constant. In other words, the leaves deviate from their closest encompassed relative by only a small amount on average. The elected schema describes this smaller hull.
Generation information can be used to determine when each part of the search space covered by the GA was considered. This information is very useful in detecting premature convergence, finding local minima, and computing the relative longevity of a subspace. The search space itself can be carved into approximately equally populated subsections by chopping the tree at nodes having a certain maximum weight. Analysis of these subsections across dimensions of fitness and longevity sheds light on the search space.
All of this processed information is available on-line. If desired, any case can be displayed. Also available is the tree information in graphical form with case numbers in their proper locations. The graphics are expandable so that subtrees can be thoroughly investigated. The ``report'' is meant for user consumption and usually raises some questions which can be answered by pulling more information from the system.
It is important to emphasize that the system is an interactive tool for use in explaining GA-generated solutions. Although it automates the information extraction and processing to some extent, human perception is a critical ingredient in the final analysis. However, without the reasonable organization and pre-processing that this system provides, the large amount of data created during a GA run is impossible to digest even for an experienced GA researcher.
Several experiments in function optimization and circuit design show that clustering techniques, if properly applied, provide a strong case-base, yielding useful data about the GA run. These results are reported in more detail in [Louis et al., 1993]. A simple example (f(x) = x) in function optimization introduces the system and provides a methodology for analyzing the information in the report. Next, a design example from a genetic-algorithm-generated circuit for a 5-bit parity checker supports the methodology and results obtained through the system.
The tree structure resulting from clustering defines a schema hierarchy
(figures and ). Schemas of lower order are found near
the top of the tree. Schema order gets higher and higher towards the leaves,
which, with all alleles fixed, have the maximum possible order.
Figure depicts the index tree of an entire case-base for
maximizing a simple function: f(x)=x. Some salient features of the space are
immediately recognizable on the graph (when one can zoom in and look at cases).
These features are marked in figure . Figure shows an
enlargement of the small boxed area in figure (labeled ``Area of
Detail''). In this figure, the positions of both initial cases (individuals)
to the right of the figure and abstract cases at the internal nodes are
represented by their schemas. Schemas closer to the root of the tree are more
general (that is, of lower order) than those towards the leaves.
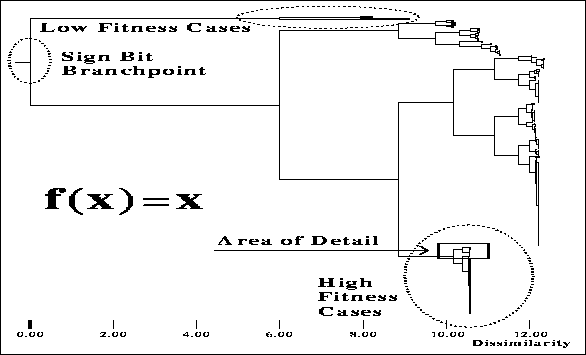
Figure: Tree structure of the cases. Nodes represent
abstracted cases.
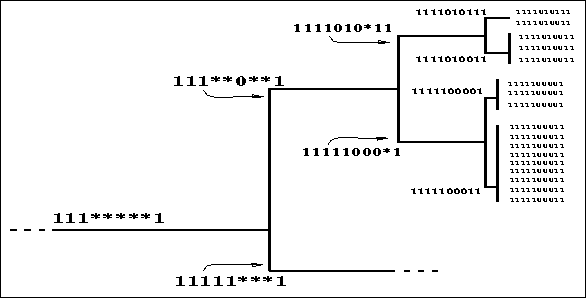
Figure: A closer look at the clustered cases reveals nested
schemas.
The case-base was created by clustering the 400 GA individuals from the first
20 generations (which resulted in a binary tree) and then computing the
abstract cases at the internal nodes. The resulting case-base had 799 cases,
400 of which came directly from the GA. The salient features in the search
space, like the importance of the sign bit, can be identified and marked using
the report mentioned above in conjunction with the index-tree graph.
Clustering partitions the individuals into sets sharing common features, namely
specific allele values (syntactic similarity) and similar fitness. In this
case, all the low-fitness cases are clumped together toward the top of the
graph. The high-fitness cases are at the bottom. A sign bit was used in the
genotype (values ranged from -511 to 511). The sign-bit branching point is
shown in figure as well. Not surprisingly, all the negative
numbers are clustered together above the sign-bit branchpoint, and very little
time was spent in that portion (half) of the search space by the GA. This
information was discovered by zooming in on the subsections of the graph and
noting the obvious common features while consulting the on-line case-base.
Case zero is located at the root of the tree. Actual output from a query shows case-information:
> (show-case 0) +--------------------------------------------------------------+ | Case: 0 | Distance: 0 Weight: 400 Fitness: 8441.44 | |------------+ Order: 0 Schema: ********** | | Additive schema: (396 333 170 283 338 330 20 72 332 392) | | Longevity: 19 (lo:1 avg:10.5 hi:20) | | Left subtree: 1 Right subtree: 396 | +---------------------------------------------------------------
Since case 0 is located at the root of the tree, its distance from the root is 0. There are 400 leaves below it, making its weight 400. Fitness is calculated by averaging the fitnesses of the cases below. The case schema is filled with ``*''s, showing once again why the additive schema information is important. Leaves under case 0 spanned all generations from 1 to 20 resulting in a longevity value of 19. Case 0 has two pointers, one to case 1 and another to case 396. This reflects the binary nature of the index. Had the case been a leaf it would not have pointed to further cases.
Experiments in function optimization (summarized in section ), combined
with genetic algorithm theory, indicate that a useful high-level description of
the case-base and the search recorded within it can be generated as follows:
The parity-checker problem's search space is poorly understood, discontinuous,
and highly non-linear. As encoded for the GA, a 5-bit parity-checker problem
results in a 
sized search space having these troublesome properties.
The experiments used a genotype of length 80, and a population size of 20,
and ran the GA for 25 generations. Appendix contains a plot
of the cluster tree, and an abbreviated report for the 5-bit parity-checker
problem from chapter , along with instructions for
obtaining the public domain code for clustering. The analysis below uses the
report, cluster tree (figure ), and figure .
The GA does not solve the problem in 25 generations. In the experiments, a
case-base was created by clustering the 500 individuals created by the GA and
computing the 499 abstract cases (see figure in
appendix ). The analysis proceeded by examining the report and
following the steps outlined in the methodology section. The disjoint subtree
list was then inspected. The strongest such subtree (H) was also heavily
weighted and spanned many generations. In addition, the best partial solutions
all fell within H. This implied that a complete solution would fit H's
schema. Since the order of the schema was appreciable (38 of 80), the
search could be constrained to that schema in the hope of finding a solution.
One correct solution was in fact contained within H's schema.
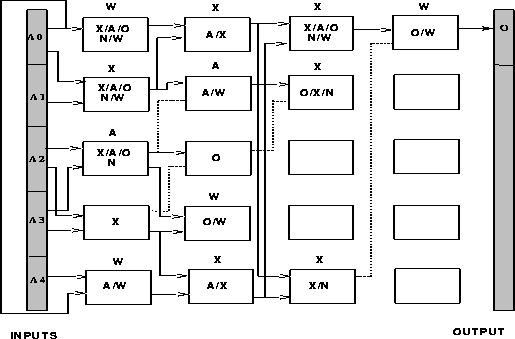
Figure: Parity circuit indicated by H, and the correct instantiation of
choices.
Figure shows the circuit indicated by the previous analysis of
H. By decoding H, it was possible to discern the general structure of a
solution and determine which parts of it were important. Labeled boxes
represent one of the logic gates eXclusive-or, And, Or,
Not, and Wire. Since the circuit in figure represents a
schema, multiple labels on the boxes show its possible instantiations. Labels
above boxes represent a correct instantiation found near the 
generation of an unconstrained run. The top row should be considered adjacent
to the bottom.
Since gates form easily recognizable building blocks, the low-order schemas
corresponding to boxes whose inputs are not fixed denote unimportant gates. The
unlabeled boxes thus reflect unimportant dimensions of the search space, which
can be safely ignored. Recall from chapter that gates
have two inputs, one of which is determined by the genetic algorithm. The
figure and report imply that gates participating in a correct solution had
already fixed their input locations by generation 25. Thus the alleles
specifying input location denote an important building block. The search space
size also decreases significantly, since the schemas that specify unlabelled
boxes, and the already fixed positions in H at generation 25, can be
ignored. In fact, the search space size decreases by approximately 15 orders
of magnitude. Additionally, of the 10 schemas corresponding to boxes whose
inputs are fixed, nine can specify an eXclusive-or. These gates are
important for a parity checker. Finally, genetic algorithm theory implies that
the higher the fitness of a schema, the earlier that schema is fixed (dominates
the population). Therefore the gates and inputs that were fixed earlier in the
search for a circuit will tend to cause greater changes in performance compared
to gates that were fixed later during the search.
Results presented here are a summary of the more extensive work reported
in [Louis et al., 1993]. Testing on a series of optimization problems including the
DeJong [DeJong, 1975] functions and a pair of deceptive problems shows that the
CBR tools are useful for understanding GA solutions in many different kinds of
spaces as exemplified by the test problems. These functions are given in
table and range from linear to exponential. The three functions
from the DeJong test suite for genetic algorithms [DeJong, 1975] provide
multimodal and discontinuous spaces.
Evidence of the GA's path through the search space can be seen. Many of the earlier subtrees may have low average fitness and low order, whereas later subtrees will have higher order if convergence was approached. Typically, later nodes have higher fitness, but as clustering is sensitive to genotype, it is possible to have a weak but young subtree.
Low-order long-lived subtrees with poor fitness are often associated with crippled individuals formed by mutation or unfortunate crossover. If there are many weak subtrees, one can infer a stronger focus on exploration of new parts of the space as opposed to exploitation of strong, higher-order schema. The schemas defined by such subtrees denote unpromising areas of the space.
High-order short-lived subtrees offer evidence of temporary concentration of search effort, which often follows discovery of a beneficial building block. Once a building block has been incorporated into the population (exploited), the search effort may move on to further exploration.
In problems where there is deception (that is, where most of the gradient in the space draws the GA away from the absolute global optimum but toward some local optimum), a user of this system would expect to see the GA focus first on the local maximum. If the GA manages to discover points near enough to the global maximum that they are favorably evaluated, a paradigm shift may occur. This has been evident in the case-bases.
If a user notices that a small but strong subtree was discovered but quickly lost and not surpassed, that might suggest a need for alteration of the GA parameters in favor of a more elitist selection strategy (like CHC). When there is suspicion of deception, it may be confirmed or discredited by looking at the lower levels of the quickly lost cluster. If it is discovered that within the cluster, the later and stronger subclusters had schema changes that appeared to cause relative decline in other contemporary clusters, then there is stronger evidence for deception. At this point a more thorough investigation of that part of the search space without much competition is justified.
Motivations for including a hypothesis generator are many. If hypothesis-produced individuals prove to be better on average than GA-produced individuals, the GA will be accelerated. They also provide evidence that produced solutions are reasonably well understood. Further support is furnished by the identification of building blocks.
Work on hypothesis generation focuses on using the principled heuristics
sketched in section . The convex hull of each subtree selected by
the method outlined there contains a very large number of possible individuals
that have never been evaluated. The hypothesis module picks some specific
individuals from within the hull of the most promising subtree and injects them
for participation and evaluation within the GA population. Only a small number
of generated individuals are injected in a given generation.
Since individuals that fit in the reduced hull of the elected schema may be considered more prototypical of the subtree than those that do not, the elected schema provides a better template for the generator than does the regular schema. Hypotheses are therefore chosen from this reduced hull.
Finally, consider cases where a small but strong cluster is discovered but quickly swamped by outside evolutionary pressures. Injection of some new members of the ``lost'' subspace into the population may help, as the undersampled space may deserve further investigation.
In each of the solution spaces searched by the GA, hypothesis injection on
average provided detectable and reproducible improvements. Even though
injection was performed only twice per experiment, hamming distance to the
optimal solution was decreased by more than 
of the problem size
over the baseline case. A GA converges when the average hamming distance
between individuals in a population stabilizes (see
chapter ). In several instances, the solution was
discovered within one generation of the injection. In experiments, the GA
converged more quickly and to better solutions when hypothesis injection was
used.
Hypotheses generated by CBR tools can provide principled direction to otherwise less-productive GA search as well as help in the avoidance of deception. Although it is possible to damage the search through hypothesis injection, this risk can be reduced by meta-level application of CBR techniques. In the future, the hypothesis generator should track the progress of genetically engineered individuals and update its knowledge base. Hypothesis injection should also be continuous with a small number of individuals injected every generation and their progress tracked.
The system described in this chapter provides a tool with which users can explain discovered solutions while simultaneously discovering important aspects of the search space. Tools and techniques from case-based reasoning are able to make explicit the building blocks used by a GA. Analysis of the building blocks and the path taken by a GA through a search space provides a powerful explanatory mechanism. Salient features are apparent from the structure of the graph and are important for increasing understanding of poorly-understood functions. The explanation can be used to guide post-processing in order to improve results in case of premature convergence or no convergence.
During subsequent attempts at the task of designing a parity checker, search
space size could be reduced, building blocks identified, and unimportant areas
of the search space avoided The importance of the eXclusive-or, input
location choice, and the unimportance of certain positions (unlabeled boxes in
figure ) provides useful knowledge to a designer. The system also
allows sensitivity analysis based on genetic algorithm theory. The GA theory
implies that schemas discovered earlier cause greater changes in performance
compared to schemas that were discovered later.
As well as providing a system for GA explanation and search space analysis, the
system provides empirical evidence that the building block hypothesis is
correct, at least for the functions in table . As mentioned
above, the hierarchical clustering of a set of GA individuals (distributed over
several generations) according to fitness and genotype leads to nested schemas.
Analysis shows that the subtrees with the most fit schemas receive the most
reproductive energy while the least fit schemas are culled from the population.
Although theory said that clustering on fitness and genotype should yield
nested schemas (as a result of the building block hypothesis), the system was
nonetheless tested on several other clustering possibilities, including more
generational information and parental information. Clustering on fitness and
genotype was by far the most successful technique. The nested schemas that
result from such a clustering provide a coherent index for the case-base.
Although the time complexity of the fitness function may be known, the problem in this thesis is to put bounds on the number of generations until convergence. A computational tool must be able to bound time complexity. The next chapter addresses this issue.
