Each type of knowledge needs some form of ``representation'' and a body of skills adapted to using that style of representation.- Marvin Minsky. Society of Mind. 1985
This chapter describes the assumptions behind the principle of meaningful building blocks and defines a new crossover operator that relaxes these assumptions. The new operator makes choosing a GA encoding easier, paving the way for applying GAs in design. The chapter uses design problems from combinational circuit design (designing adders and parity checkers) to illustrate the results.
The search bias during genetic search depends on: the problem, the structure of the encoded search space for the problem, and the genetic operators of selection, crossover, and mutation. For every problem there are a large number of possible encodings. It is often possible to follow the principle of minimal alphabets when choosing an encoding for a genetic algorithm, but simultaneously following the principle of meaningful building blocks can be much harder. This is because our intuition about the structure of the problem space may not translate well in the binary-encoded spaces that genetic algorithms thrive on.
There are two possible ways of tackling the problem of coding design for meaningful building blocks.
The first choice uses reordering operators, like inversion, that change the encoding while searching for the solution and is discussed next. The rest of the chapter motivates, develops and illustrates the second approach.
Inversion rearranges the bits in a string allowing linked bits to move close
together (see figure ![]() ).
).
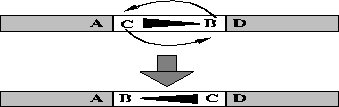
Figure: Inversion. Notice that after inversion ``A'' is close to ``B''
Inversion occurs in nature and serves a similar function. Genes and their alleles are linked if their expression is dependent on one another. Tight linkage is established when linked alleles are close together and such alleles are called co-adapted alleles. Epistasis is the term used to describe the degree of linkage among alleles. In genetic algorithms, inversion is implemented by changing the encoding to carry along a tag which identifies the position of a bit in the string [Goldberg, 1989b]. With the tags specifying position, it is now possible to cut and splice parts of a string allowing bits to migrate and come together. Inversion-like reordering operators have been implemented by Goldberg and others [Goldberg and Lingle, 1985, Smith, 1985] with some good results.
The problem with using inversion and inversion-like operators is the decrease
in computational feasibility. If l is the length of a string, inversion
increases the search space from ![]() to
to ![]() . Natural selection has
geological time scales to work with and therefore inversion is sufficient to
generate tight linkage. Designers do not have this amount of time or the
resources available to nature.
. Natural selection has
geological time scales to work with and therefore inversion is sufficient to
generate tight linkage. Designers do not have this amount of time or the
resources available to nature.
Instead of using reordering operators, this thesis expands the number of encodings that a genetic algorithm finds useful by increasing the types of building bocks considered meaningful by a genetic algorithm.
The principle of meaningful building blocks (stated in chapter ![]() ,
section
,
section ![]() ) arises mainly from the search biases generated by the
crossover operator. To see why, consider the probability of disruption of a
schema. Let H be a schema,
) arises mainly from the search biases generated by the
crossover operator. To see why, consider the probability of disruption of a
schema. Let H be a schema, ![]() its defining length and O(H) its
order. Then the probability that the crossover point falls within the schema is
its defining length and O(H) its
order. Then the probability that the crossover point falls within the schema is
![]() where l is the length of the string containing the schema.
This is the second term in equation
where l is the length of the string containing the schema.
This is the second term in equation ![]() and is the probability that
crossover will disrupt the schema. Since the probability of disruption is
proportional to the defining length, schemas of long defining length tend to be
disrupted more often than their shorter counterparts. Consequently, the
principle of meaningful building blocks tries to ensure that a chosen encoding
does not have long building blocks. However, the mapping from genotype to
phenotype is in general much more complex in design, hence it may not be known
whether the encoding follows the principle of meaningful building blocks even
when the underlying domain is relatively well understood. This means that
schemas of arbitrary defining length may need to be preserved and the bias
towards short schemas becomes a liability.
and is the probability that
crossover will disrupt the schema. Since the probability of disruption is
proportional to the defining length, schemas of long defining length tend to be
disrupted more often than their shorter counterparts. Consequently, the
principle of meaningful building blocks tries to ensure that a chosen encoding
does not have long building blocks. However, the mapping from genotype to
phenotype is in general much more complex in design, hence it may not be known
whether the encoding follows the principle of meaningful building blocks even
when the underlying domain is relatively well understood. This means that
schemas of arbitrary defining length may need to be preserved and the bias
towards short schemas becomes a liability.
One way of combating the problem of disruption of long schemas in the encoding of design problems is to remove the bias toward short schemas and allow low order schemas of arbitrary defining length to bias search in useful directions.
Previous approaches to this problem used a new crossover operator like punctuated crossover or uniform crossover. Punctuated crossover relies on a binary mask, carried along as part of the genotype, in which a `1' identifies a crossover point. Masks, being part of the genotypic string, change through crossover and mutation. Experimental results with punctuated crossover did not conclusively prove the usefulness of this operator or whether these masks adapt to an encoding [Schaeffer and Morishima, 1987, Schaeffer and Morishima, 1988].
Uniform crossover exchanges every corresponding pair of bits with a probability of 0.5. The probability of disruption of a schema is now proportional to the order of the schema and independent of defining length. Experimental results with uniform crossover suggest that this property may be useful in some problems [Syswerda, 1989]. However, in design problems the idea is not to disrupt a highly fit schema whatever its defining length.
A second point needs to be made. Natural selection works by biasing search in any direction that shows the slightest improvement in survivability. This directional information is implicit in the number of competing alleles that exist in a population, and in nature, cannot be stored anywhere. Classical genetic algorithms and their operators, mimicking natural selection, are also bound by these constraints.
In summary, designing an encoding is complex and something of an art. To solve the problem of bad taste on the part of GA programmers, or at least to give them more leeway, this thesis lets the GA exploit encodings that are less constrained. The following sections describe and use a masked crossover operator to remove the bias toward short schemas and to make use of explicitly stored directional information to efficiently bias search.
The assumption that short, low-order schemas are needed to solve a problem is dependent on the encoding and the crossover operator. A strategy that identifies highly fit schemas or building blocks of arbitrary defining length would expand the set of possible encodings with which a GA could work, leading perhaps to a lower aesthetic threshold for GA programmers.
The operator that introduces bias due to the encoding in genetic search is crossover. Various alternatives to the classical crossover operators have been proposed and studied [Schaeffer et al., 1991, Syswerda, 1989]. Syswerda's paper concludes that there are no clear winners, but when in doubt, use uniform crossover. It is clear, however, that for all the operators studied, some do better on certain problems and worse on others, indicating that the biases introduced are problem/encoding dependent. An adaptive crossover operator that adapts to the encoding, being able to exploit information unused by classical crossover operators, may be better than classical crossover operators. The cost to be paid for adaptive crossover lies in the added complexity of the operator and the paradoxical point that it can be more easily misled. The more information that an algorithm looks at, the more its trajectory can be affected by bad leads. A genetic algorithm using classical crossover is less likely to be misled than a genetic algorithm using adaptive crossover since classical crossover ignores information used by adaptive crossover and is thus immune to misdirection in this information.
Simple non-adaptive crossover, the classical crossover operator, consists of choosing a point in the string and following the procedure outlined below:
for ¯i from 1 to crossover-pointbegin
Copy gene to child1[i] from parent1[i]
Copy gene to child2[i] from parent2[i]
end
for i from (crossover-point + 1) to Chromosome-length
begin
Copy gene to child1[i] from parent2[i]
Copy gene to child2[i] from parent1[i]
end
One point crossover, and variants thereof, limit the number of encodings that a genetic algorithm can exploit because they assume that contiguous genes form building blocks. With adaptive crossover, this constraint should be relaxed.
For the search process to exploit any information in the encoding, the crossover operator needs to be able to preserve highly fit schemas, no matter what their length. This suggests a masking scheme, in which the positions making up highly fit schemas are identified, tagged and preserved. Masks can be propagated in two ways.
This dissertation defines an operator that directly makes use of the relative fitness of the children, with respect to their parents, to guide crossover. The relative fitness of the children indicates the desirability of proceeding in a particular search direction. The use of this information is not limited to our operator, and can be used in classical GAs with minor modifications (or example, one way to improve traditional crossover operators is to keep a sorted list of previous crossover points that produced highly fit children).
Masked crossover (MX) uses binary masks to direct crossover. Let A and B be
the two parent strings, and let C and D be the two children produced.
Mask1 and Mask2 are a binary mask pair, where Mask1 is associated with
A and Mask2 with B. A subscript indicates a bit position in a string.
Masked crossover is shown in figure ![]() and defined below:
and defined below:
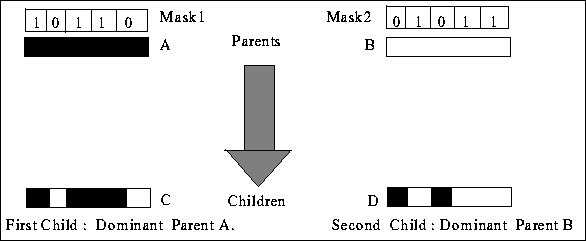
Figure: Masked crossover. The bits that are exchanged depend on the masks.
This allows preservation of schemas of arbitrary defining length
copy A to C and B to Dfor ¯i from 1 to string-length
begin
if ¯
and
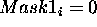
copy the
bit from B to C
if ¯
and
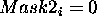
copy the
bit from A to D
end
First, it is easy to see that traditional crossover operators are special cases
of MX. One-point crossover (figure ![]() ) can be implemented by simply
setting the first n bits (n < length of string) of M1 to 1 and the
rest to 0, M2 being the complement of M1. For uniform crossover, the
) can be implemented by simply
setting the first n bits (n < length of string) of M1 to 1 and the
rest to 0, M2 being the complement of M1. For uniform crossover, the
![]() bit of M1 is decided by a fair coin toss, M2 again being the
complement. This allows the disruptiveness of MX to range from that of one
point to that of uniform crossover.
bit of M1 is decided by a fair coin toss, M2 again being the
complement. This allows the disruptiveness of MX to range from that of one
point to that of uniform crossover.
Masked crossover tries to preserve schemas identified by the masks. Let A be called the dominant parent with respect to C, and B the dominant parent with respect to D. This follows from the definition of masked crossover since during production of C, when corresponding bits of A and B are the same, the bit from A is copied to C.
Intuitively, 1's in the mask (probabilistically) signify bits participating in highly fit schemas. MX preserves A's schemas in C while adding some schemas from B at those positions that A has not fixed. A similar process produces D. Search biasing is done by changing masks in succeeding generations. Instead of using genetic operators on masks, this thesis uses a set of rules that operate bitwise on parent masks to control future mask settings. Since crossover is controlled by masks, using meta-masks to control mask string crossover then leads to meta-meta masks and so on. Using rules for mask propagation avoids this problem. Choosing the rule to be used is dependent on the fitness of the child relative to that of its parents.
Three types of children can be defined:
With two children produced by each crossover and three types of
children, there are a total of ![]() or nine possibilities, with associated
interpretations and possible actions on the masks. However, since the order of
choosing children does not matter, the number of cases falls to six (see
figure
or nine possibilities, with associated
interpretations and possible actions on the masks. However, since the order of
choosing children does not matter, the number of cases falls to six (see
figure ![]() ).
).
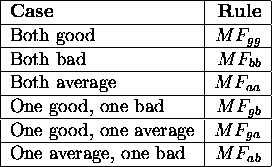
Figure: Six ways of pairing children and their associated mask functions/rules
(MF).
This section specifies rules for mask propagation. In each case a child's mask
is a copy of the dominant parent's except for the changes the rules allow. The
underlying premise guiding the rules is that when a child is less fit than its
dominant parent, the recessive parent contributed bits deleterious to its
fitness. Encouraging search in the area defined by these loci, the idea is to
search in areas close to one parent with information from the other parent
providing some guidance.![]() A mask mutation operator that flips a mask bit with low
probability is assumed to act during mask propagation. To illustrate a mask
function and to give some intuition, the mask function for
A mask mutation operator that flips a mask bit with low
probability is assumed to act during mask propagation. To illustrate a mask
function and to give some intuition, the mask function for ![]() , when both
children are good, is described below. Appendix
, when both
children are good, is described below. Appendix ![]() contains the
complete set of mask rules used in this chapter.
contains the
complete set of mask rules used in this chapter.
Let P1 and P2 be the two parents, PM1 and PM2 their respective masks. Similarly, C1 and C2 are the two children with masks CM1 and CM2. The modifications to masks depend on the relative ordering of P1, P2, C1 and C2. In this section's figure, the ``#'' represents positions decided by tossing a coin.
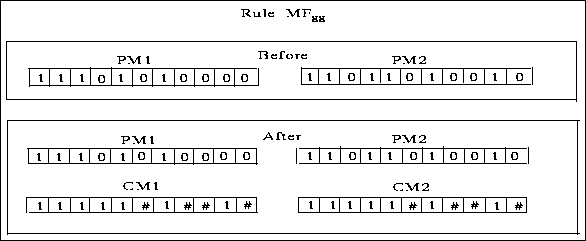
Figure: Mask rule ![]() : Example of mask propagation when both C1 and C2
are good
: Example of mask propagation when both C1 and C2
are good
The mask functions in appendix ![]() are examples from one of several
different sets of possible rules, since many mask propagation rules can be
defined. In fact a GA can search the space of mask rules to find a suitable set
if an evaluation function can be attached to the masks. This may be overkill,
since the number of rules is usually small enough that simpler methods will
suffice.
are examples from one of several
different sets of possible rules, since many mask propagation rules can be
defined. In fact a GA can search the space of mask rules to find a suitable set
if an evaluation function can be attached to the masks. This may be overkill,
since the number of rules is usually small enough that simpler methods will
suffice.
With mask propagation through mask rules, directional information is explicitly stored in the masks and used by the crossover operator to bias search. The main features of the masked crossover operator are then, storage and use of directional information, and independence from defining length of schemas. Think of masked crossover as a good compromise between the disruptiveness of uniform crossover and the bias toward short schemas of classical crossover.
Masked crossover presents a problem when using classical selection procedures. The classical strategy of allowing the children produced to replace the original population will not allow a genetic algorithm using masked crossover to converge. Masks will tend to disrupt the best individuals while searching for promising directions to explore because of the nature of the rules guiding mask propagation. Therefore, the selection procedure used, is a modification of the CHC selection strategy, in which, if the population size is N, the children produced double the population to 2N. From this population of 2N, the N best individuals are chosen for further consideration [Eshelman, 1991]. This elitist selection strategy is used to enhance convergence. Another problem which may occur is that although MX preserves schemas of arbitrary defining length, the fitness information itself may be misleading. Such problems are called deceptive. When fitness information is misleading, a GA using masked crossover can be expected to perform worse than a GA using crossover operators that do not use such information. This is borne out by results from the adder problem.
A performance difference due to selection should be expected since fitness information biases CHC selection more than traditional selection. The elitist selection strategy used here results in a stronger focus on exploitation of the search space at the cost of reduced exploration. Less exploration implies a reduced emphasis on crossover (crossover explores the space). Crossover's smaller role leads to decreased epistatic effects since epistasis only influences crossover. Whatever the crossover operator used, the CHC selection strategy should increase performance, but again at the cost of increasing susceptibility to deception. Results presented in the next section illustrate the effects of selection strategy.
A Designer Genetic Algorithm (DGA) therefore differs from a classical genetic algorithm both in the crossover operator (masked crossover) and in the selection strategy (elitist) used.
A designer genetic algorithm's performance is compared with that of a classical GA on the adder and parity problems. In all experiments, the population is made up of 30 genotypes. The probability of crossover is 0.7 and the probability of mutation is 0.04. These numbers were found to be optimal through a series of experiments using various population sizes and probabilities. The graphs in this section plot maximum and average fitnesses over ten runs.
Each genotype is a bit string that maps to a two-dimensional structure
(phenotype) embodying a circuit as shown in figures ![]() and
and ![]() .
.
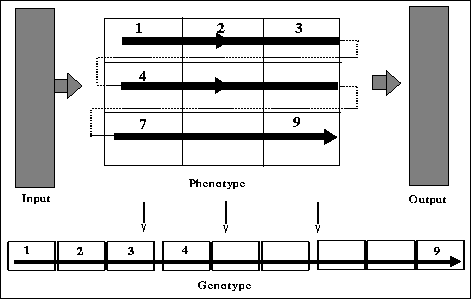
Figure: A mapping from a two-dimensional phenotypic structure (circuit) to
position in a one-dimensional genotype.
3 bits are needed to represent 8 possible gates. A gate has two inputs and
one output. Considering the phenotype as a two dimensional array of gates S,
a gate ![]() , gets its first input from
, gets its first input from ![]() and its second, from
one of
and its second, from
one of ![]() or
or ![]() as shown in figure
as shown in figure ![]() .
.
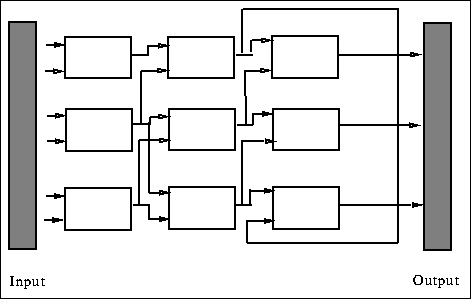
Figure: A gate in a two-dimensional template gets its second input
from either one of two gates in the previous column.
An additional bit associated with each gate encodes this choice. If the gate is
in the first or last rows, the row number for the second input is calculated
modulo the number of rows. The gates in the first column, ![]() receive
the input to the circuit. Connecting wires are simply gates that transfer one
of their inputs to their output. The other gates are AND, OR (inclusive OR),
NOT and XOR (exclusive OR).
receive
the input to the circuit. Connecting wires are simply gates that transfer one
of their inputs to their output. The other gates are AND, OR (inclusive OR),
NOT and XOR (exclusive OR).
The fitness of a genotype is determined by evaluating the associated phenotypic
structure that specifies a circuit. If the number of bits is n, the circuit
is tested on the ![]() possible combinations of n bits. The fitness function
returns the sum of the correct responses. This sum is maximized by the
algorithm. For the 4-bit parity checker, the binary numbers 0 to 15 are
inputs to the decoded circuit. If the circuit is correct, its fitness is 16,
which means that the circuit correctly finds the parity of all the 16
possible 4-bit numbers. For the adder problem the input is a set of 2,
n-bit numbers. The output is an n+1 bit sum. For a 2-bit adder, the maximum
fitness would be
possible combinations of n bits. The fitness function
returns the sum of the correct responses. This sum is maximized by the
algorithm. For the 4-bit parity checker, the binary numbers 0 to 15 are
inputs to the decoded circuit. If the circuit is correct, its fitness is 16,
which means that the circuit correctly finds the parity of all the 16
possible 4-bit numbers. For the adder problem the input is a set of 2,
n-bit numbers. The output is an n+1 bit sum. For a 2-bit adder, the maximum
fitness would be ![]() or 48. Note that in contrast to optimization
problems, the maximum fitness is known -- the algorithm searches for a
structure (circuit) that achieves this maximum fitness.
or 48. Note that in contrast to optimization
problems, the maximum fitness is known -- the algorithm searches for a
structure (circuit) that achieves this maximum fitness.
When comparing the performance of a classical GA using elitist selection with a
DGA on a 2-bit adder problem, the graphs in figures ![]() and
and ![]() show that the classical GA does better, although the
difference is not great. This is not very encouraging.
However, implementing the carry bit makes the solution space of the adder
problem deceptive. A problem is deceptive to a GA when highly fit low-order
schemas lead away from highly fit schemas of higher order. As explained
earlier, since MX uses fitness information to bias search, it is more easily
misled than traditional crossover.
show that the classical GA does better, although the
difference is not great. This is not very encouraging.
However, implementing the carry bit makes the solution space of the adder
problem deceptive. A problem is deceptive to a GA when highly fit low-order
schemas lead away from highly fit schemas of higher order. As explained
earlier, since MX uses fitness information to bias search, it is more easily
misled than traditional crossover.
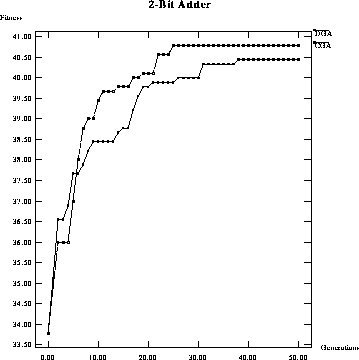
Figure: Performance comparison of maximum fitness per generation of a
classical GA versus a DGA on a 2-bit adder.

Figure: Performance comparison of average fitness per generation of a
classical GA versus a DGA on a 2-bit adder.
Although a problem is deceptive, it does not mean that no solutions can be
found. Figures ![]() and
and ![]() show solutions to the
2-bit adder problem found by a designer genetic algorithm and classical genetic
algorithm. As wire gates ignore their second input, only one input is shown for
such gates. The gate in the third row and third column (
show solutions to the
2-bit adder problem found by a designer genetic algorithm and classical genetic
algorithm. As wire gates ignore their second input, only one input is shown for
such gates. The gate in the third row and third column ( ![]() ) is shown
unconnected because it does not affect the output.
) is shown
unconnected because it does not affect the output.
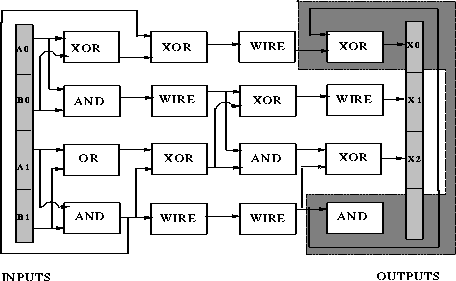
Figure: A 2-bit adder designed by a designer genetic algorithm.
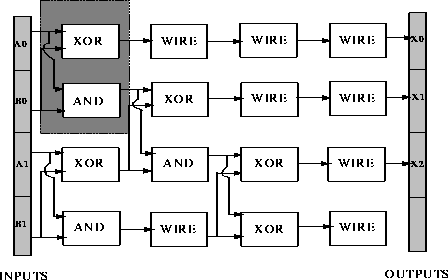
Figure: A 2-bit adder designed by a classical genetic algorithm.
In figures ![]() and
and ![]() the shaded regions
represent highly fit schemas. Notice that the DGA preserves a schema of much
longer length than the CGA. Additionally the figures illustrate the difficulty
of understanding why the circuit works. The problem of opacity of GA-generated
solutions is handled in the next chapter.
the shaded regions
represent highly fit schemas. Notice that the DGA preserves a schema of much
longer length than the CGA. Additionally the figures illustrate the difficulty
of understanding why the circuit works. The problem of opacity of GA-generated
solutions is handled in the next chapter.
Now consider the parity problem. The encoding described in figure ![]() will violate the principle of meaningful building blocks with regard to the
solution to the parity problem as shown in figure
will violate the principle of meaningful building blocks with regard to the
solution to the parity problem as shown in figure ![]() . Since
diagonal elements of S (the 2-D phenotype) are further apart in the
one-dimensional genotypic string, any good subsolutions (highly fit, low-order
schemas) found will tend to be disrupted by traditional crossover.
. Since
diagonal elements of S (the 2-D phenotype) are further apart in the
one-dimensional genotypic string, any good subsolutions (highly fit, low-order
schemas) found will tend to be disrupted by traditional crossover.
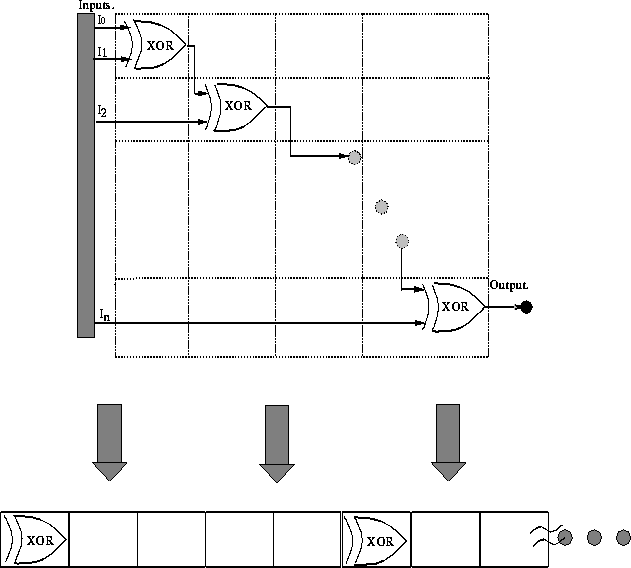
Figure: The XOR gates that are close together (diagonally) in the
two-dimensional grid will be far apart when mapped to a one-dimensional
genotype
In other words, gates which are close together in two-dimensional (phenotype)
space may be far apart in one-dimensional (genotype) space, causing problems
for classical GAs. MX, however, will find and preserve these subsolutions as
its performance is independent of defining length. To observe performance under
these conditions, the experiments restrict the number of gate types available
to the GA to three and do not allow a choice of input (the second input is now
always from the next row, modulo the number of rows). Although this reduces
the size of the search space, traditional crossover disrupts low-order schemas
and therefore performs worse than the DGA. Figure ![]() and
figure
and
figure ![]() show this for a 4-bit parity checker. (In cases where
there were no restrictions the performance of both GAs was comparable.)
show this for a 4-bit parity checker. (In cases where
there were no restrictions the performance of both GAs was comparable.)
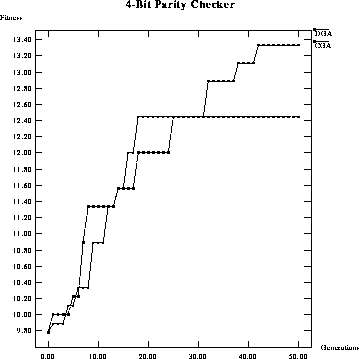
Figure: Performance comparison of maximum fitness per generation of a
classical GA versus a DGA on a 4-bit parity checker.
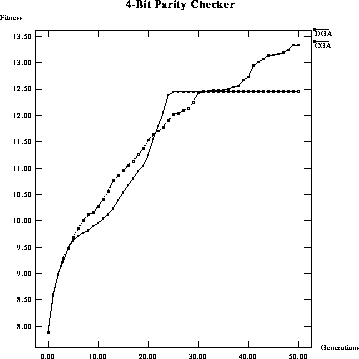
Figure: Performance comparison of average fitness per generation of a
classical GA versus a DGA on a 4-bit parity checker.
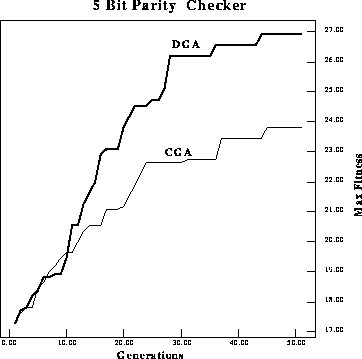
Figure: Performance comparison of maximum fitness per generation of a
classical GA versus a DGA on a 5-bit parity checker.
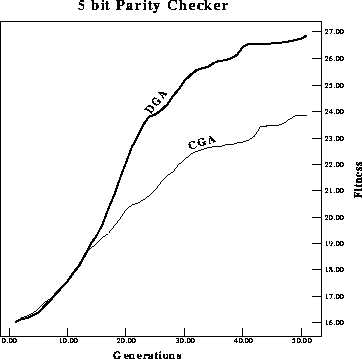
Figure: Performance comparison of average fitness per generation of a
classical GA versus a DGA on a 5-bit parity checker.
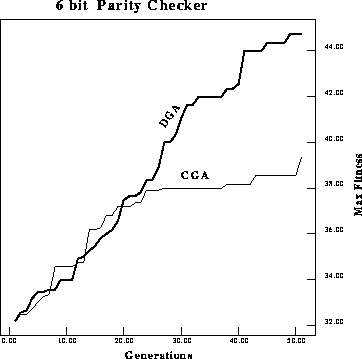
Figure: Performance comparison of maximum fitness per generation of a
classical GA versus a DGA on a 6-bit parity checker.
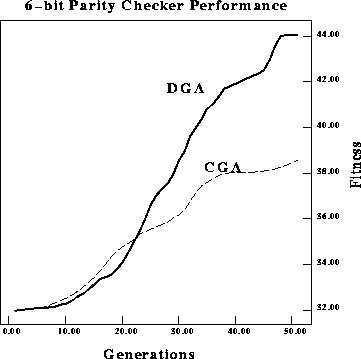
Figure: Performance comparison of average fitness per generation of a
classical GA versus a DGA on a 6-bit parity checker.
As expected, the difference in performance gets larger as the problem is scaled
in size. Figure ![]() and figure
and figure ![]() compare the maximum
and average fitness performance on a 5-bit problem. In the 5-bit experiments
the choice of gates was still restricted to the same three as in the previous
example.
When all possible gates are allowed, the performance
difference is less, and is due to the large increase in the number of possible
solutions and therefore a lesser degree of violation of the meaningful building
block principle (see figures
compare the maximum
and average fitness performance on a 5-bit problem. In the 5-bit experiments
the choice of gates was still restricted to the same three as in the previous
example.
When all possible gates are allowed, the performance
difference is less, and is due to the large increase in the number of possible
solutions and therefore a lesser degree of violation of the meaningful building
block principle (see figures ![]() and
and ![]() ).
However, as the number of solutions in a given space decreases, masked
crossover does better than traditional crossover because it uses differential
information about child fitness to bias search independent of schema defining
length. Hypothesis testing using the student's t-test on the experimental data
from the five-bit parity checker proves that the difference in performance is
significant at a confidence level greater than
).
However, as the number of solutions in a given space decreases, masked
crossover does better than traditional crossover because it uses differential
information about child fitness to bias search independent of schema defining
length. Hypothesis testing using the student's t-test on the experimental data
from the five-bit parity checker proves that the difference in performance is
significant at a confidence level greater than ![]() .
.
On the 6-bit parity checker problem, the performance difference is still
larger. Figures ![]() and
and ![]() display the maximum and average
fitnesses. Once again the difference in performance is statistically
significant using the student's t-test at a confidence level greater than
display the maximum and average
fitnesses. Once again the difference in performance is statistically
significant using the student's t-test at a confidence level greater than
![]() . Figure
. Figure ![]() shows performance at the scale of the
fitness units (vertical axis) in the 5-bit case. The 5-bit and 6-bit
performance plots are displayed together to make the change in the
performance difference more apparent. This provides evidence that as the
length of high fitness schemas grows, the performance difference gets larger.
shows performance at the scale of the
fitness units (vertical axis) in the 5-bit case. The 5-bit and 6-bit
performance plots are displayed together to make the change in the
performance difference more apparent. This provides evidence that as the
length of high fitness schemas grows, the performance difference gets larger.
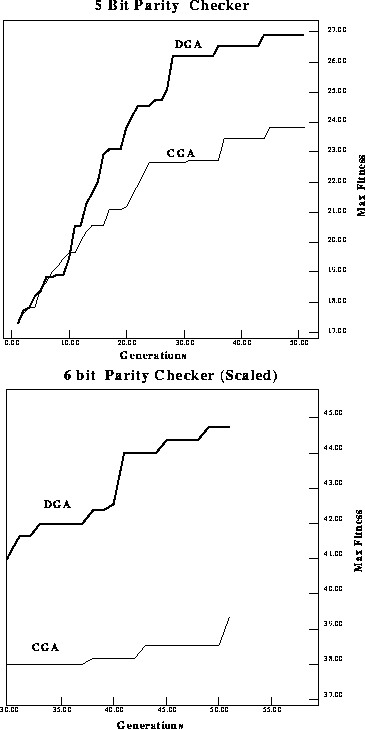
Figure: Change in performance difference as the length of high fitness schemas
(proportional to problem size) increases. Comparing a 5-bit and 6-bit parity
checker performance difference. The vertical axis for the 6-bit plot is now to
the same scale as the five bit plot. The increase in performance difference is
clearer.
In the comparisons above the effect of selection was not addressed.
Figures ![]() and
and ![]() compare the performance of:
1) a GA using traditional crossover and selection, 2) a GA using traditional
crossover and elitist selection, and 3) a DGA on a 5-bit parity problem. The
same parameter set as in the previous examples is used although setting the
number of gate types to six, increasing the number of possible solutions. This
was done in the hope of coaxing better performance from the GA using
traditional selection and crossover. The figures clearly show the importance of
selection strategy.
compare the performance of:
1) a GA using traditional crossover and selection, 2) a GA using traditional
crossover and elitist selection, and 3) a DGA on a 5-bit parity problem. The
same parameter set as in the previous examples is used although setting the
number of gate types to six, increasing the number of possible solutions. This
was done in the hope of coaxing better performance from the GA using
traditional selection and crossover. The figures clearly show the importance of
selection strategy.
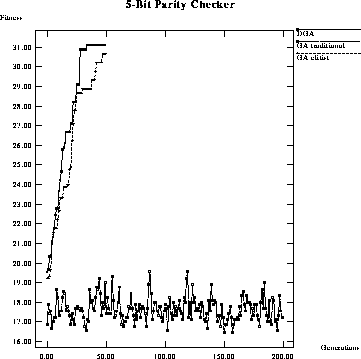
Figure: Performance comparison of maximum fitness per generation of a
classical GA using traditional selection, a classical GA with elitist
selection, and a DGA on a 5-bit parity checker.
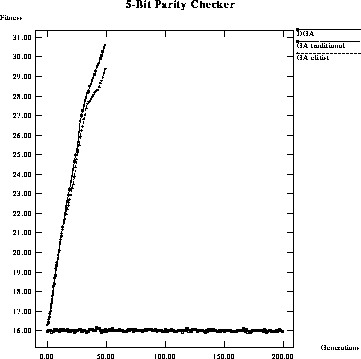
Figure: Performance comparison of average fitness per generation of a
classical GA using traditional selection, a classical GA with elitist
selection, and a DGA on a 5-bit parity checker.
The next two figures show examples of correct circuits for the 4-bit parity
problem. A DGA produced the circuit in figure ![]() and a classical
genetic algorithm produced the circuit in figure
and a classical
genetic algorithm produced the circuit in figure ![]() . The unconnected
gates in the last column do not contribute to the output, therefore their
connections have been left out. Both algorithms had the full complement of
gates available.
. The unconnected
gates in the last column do not contribute to the output, therefore their
connections have been left out. Both algorithms had the full complement of
gates available.
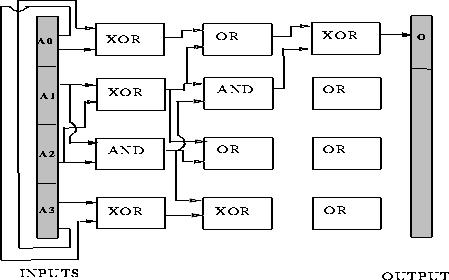
Figure: A circuit designed by a designer genetic algorithm that solves the
4-bit parity problem.
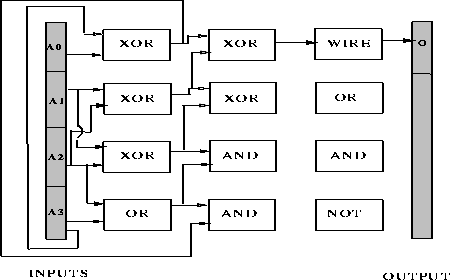
Figure: A circuit designed by a classical genetic algorithm that solves the
4-bit parity problem.
A designer genetic algorithm increases the domain of application of genetic algorithms by relaxing the emphasis on schemas of short defining length. Using masked crossover mitigates the problem of epistasis while elitist selection is crucial to good performance. This is cheaply attained since the increase in cost in using a DGA is by at most a constant factor per generation. Comparing the performance of the two GAs on a problem also gives insights about properties of the search space. If the performance difference is large, then highly fit, low-order schemas are expected to be of large defining length. Some of the circuits generated by the genetic algorithms in this chapter are not easily understandable. That is, although they can be tested for functional performance, it is not obvious how they work. In the next chapter the thesis describes a system that extracts information about the search space and uses this information to explain solutions generated by genetic algorithms.
Deception also plays a role in determining performance. Traditional crossover may do better on deceptive problems because it uses no information about search direction and is thus immune to misleading directional information.
The problem of circuit design as stated in this chapter is not an optimization problem. Since the fitness of a correct circuit, one that correctly performs the function, is known, the problem is to find a design that achieves this fitness. This is a satisficing task, not an optimization one. However, minimizing the number of gates, wires, or size of the circuit are constraints that are usually applied in practice.
Having alleviated the problem of choosing an encoding for a genetic algorithm, this thesis now considers the problem of understanding solutions generated by a genetic algorithm.