I have called this principle, by which each slight variation, if useful, is preserved, by the term of Natural Selection.-Charles Darwin. On the Origin of Species, 1859.
This chapter introduces natural selection, genetic algorithm theory, and shows the correspondence between genetic algorithms and a classical design model. This sets the stage for describing the innovative powers of a genetic algorithm and elaborating on encoding and evaluation of designs for genetic algorithms. Finally, an example from floorplanning in architecture illustrates these issues.
In its most general form, natural selection means the differential survival of
entities [Dawkins, 1986]. Some entities live and others die. For this to happen
there must be a population of entities capable of reproduction. Natural
selection prunes this population according to the criterion of survivability
(fitness). It acts as a sieve. In sexually reproducing species the unit of
natural selection is the gene. The values of a gene are its
alleles. However, sieving by itself is not capable of producing designs like
those of the life forms on this planet in any reasonable amount of time.
Natural selection needs reproducing entities to feed the results of one sieving
process on to the next, and so on. It is the continuing cycle of
reproduction and selection (the sieving process) that is responsible for the
diversity of life on earth. The existence of finite resources leads to
competition for these resources and survival of those entities that have a
competitive advantage. A life form, or phenotype, is a survival machine
built by a set of genes (a genotype) to create a competitive advantage
over other forms. Although it is the phenotypes that are directly competing for
survival, it is the genotypes that get selected on the basis of this
competition for further consideration. Evolution can be thought of as a search
process. It searches a very large space of genotypes producing structures that
are efficient at carrying out functions desirable for survival in their
environment. For example the search space for the 
X174 viral genotype is
of the order of 
, and this is one of the smallest life forms. In
1975 John Holland defined a Genetic Algorithm, a search process
based on natural selection, now used as a tool for searching the large,
poorly-understood spaces that arise in many application areas of science and
engineering [Holland, 1975].
A genetic algorithm uses the mechanics of natural selection to guide search.
It seems natural to use a genetic algorithm to design artifacts, since the
paradigm on which they are based is so successful at it. However, as already
indicated, there are difficulties and it is helpful to understand the theory
behind genetic algorithms before considering the difficulties in detail.
The algorithm was introduced in chapter 
, this chapter
considers genetic algorithm theory.
Crossover causes genotypes to be cut and spliced. This means that instead of considering the fate of individual strings in analyzing a genetic algorithm, the substrings created and manipulated by crossover must be considered. These substrings define regions of the search space and are called schemas. More formally, a schema is a template that identifies a subset of strings with similarities at certain string positions. Holland's schema theorem is fundamental to the theory of genetic algorithms. For example consider binary strings of length 6. The schema 1**0*1 describes the set of all strings of length 6 with 1s at positions 1 and 6 and a 0 at position 4. The ``*'' denotes a ``don't care'' symbol which means that positions 2, 3 and 5 can be either a 1 or a 0. Although this thesis only considers a binary alphabet, the notation can be extended to non-binary alphabets. The order of a schema is defined as the number of fixed positions in the template, while the defining length is the distance between the first and last fixed positions. The order of 1**0*1 is 3 and its defining length is 5. The fitness of a schema is the average fitness of all strings matching the schema.
A search algorithm balances the need for exploration -- to avoid local optima, with exploitation -- to converge on the optima. Genetic algorithms dynamically balance exploration versus exploitation through the recombination and selection operators respectively. With the operators as defined earlier, the schema theorem proves that relatively short, low-order, above average schema are expected to get an exponentially increasing number of trials or copies in subsequent generations [Goldberg, 1989b]. Mathematically
Here m(h,t) is the expected number of schemas h at generations t, f(h)
is the fitness of schema h and 
is the average fitness at
generation t. The genotype length is l, 
is the defining
length and O(h) the order of schema h. 
and 
are the
probabilities of crossover and mutation respectively.
The schema theorem leads to a hypothesis about the way genetic algorithms work, the building block hypothesis (bbh):
A genetic algorithm seeks near-optimal performance through the juxtaposition of short, low-order, high performance schemas or building blocks (Goldberg, 1989).This means that genetic algorithms exploit syntactic similarities in the genotype as long as the building blocks (short, high-performance schemas) lead to near-optima. The emphasis on short schemas has important consequences for encoding a problem for genetic search and is detailed in the next chapter.
Since the study of design is still in a pre-scientific stage, models provide a
limited but useful abstraction, less ambitious than theories. That is, a model
provides an abstraction of a subset of the phenomenon under consideration.
Search is the over-arching model used in this thesis and is well-established in
both artificial intelligence and design [Simon, 1969]. More specifically
genetic algorithms are used as a tool to attack the subset of design problems
stated in Chapter ; those that have an evaluation
function and can be encoded to generate candidate designs.
This section maps genetic algorithms onto an old and well-established model of
design.
One model that is widely accepted and agreed upon is the three phase model of
Asimow [Coyne et al., 1990]. The three phases are analysis, synthesis and
evaluation and a designer cycles through these phases until reaching a
satisfactory design. Analysis prepares the problem, producing an explicit
statement of goals. In GAs, this corresponds to defining the problem-dependent
evaluation function and choosing an encoding. Synthesis finds or generates
plausible solutions as carried out by crossover and mutation in genetic
algorithms. Evaluation in the three phase model judges the validity of
candidate solutions and selects among them -- selection in genetic algorithms.
The mapping is not an exact one but the linkage between the two serves to
provide a good starting point since the three phase model has already been
mapped to others [Coyne et al., 1990]. Figure shows the correspondence
between genetic algorithms and the three phase model.
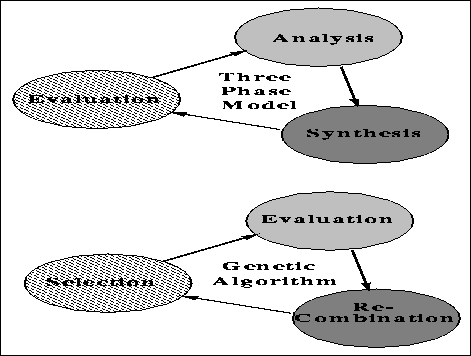
Figure: The one-to-one correspondence between the three phase model and the
genetic algorithm.
The interesting part for design is how new candidate designs are generated. In a genetic algorithm, the search bias is defined by the encoding and the genetic operators of selection, crossover and mutation. These operators make no assumptions about the continuity, differentiability or linearity of the space. Selection highlights promising areas of the space, judging candidate designs on the basis of the evaluation function. Mutation when combined with selection results in a stochastic hill-climber or gradient-descent algorithm. Crossover mixes information from many different areas of the search space and, when paired with selection, allows the combining of good partial solutions into better complete solutions. Before describing the role of the encoding and the evaluation function, this thesis establishes the innovative power of these operators.
Gero and Jo, among others [Gero and Jo, 1991, Tong and Sriram, 1992b], define two types of design activity: 1) routine or parametric design and 2) non-routine design. They further divide non-routine design into innovative and creative design. Innovativeness is characterized by unusual combinations of design variables or features while creativity introduces new design variables. These definitions and GA theory are used to show how GAs are innovative.
The building block hypothesis states that GAs work by putting together good
building blocks. Innovative designers combine concepts or ideas that worked
well in certain contexts with other ideas that worked well in other contexts to
form new, possibly better ideas which help to perform the current task. In the
same way genetic algorithms through the operations of selection and crossover
combine many different high-performance schemas (or building blocks) to form
new solutions. Mathematically, the schema theorem gives the growth rate of
high-performance schemas. As long as the disruption of these schemas due to
crossover and mutation (the last two terms in equation ) is
sufficiently small, the necessary number of building blocks are expected to be
present. Most crossover and mutation operators satisfy this requirement.
Holland's second law of genetic algorithms also quantifies the probability that
good schemas will combine through the randomized action of crossover. Suppose
m building blocks are needed to form a particular solution and each building
block has at a least P representatives in the current population of size N.
Repeated crossing over with a low disruption crossover operator implies that no
less than 
individuals have all the required m building blocks
together. Thus selection combined with crossover allows building blocks to
grow and innovatively combine into design solutions.
In its simplest form, using a genetic algorithm for design is like playing with a Meccano set (a child's construction kit). Given some low level primitives, the task is to put them together so that they perform a certain function. The genotype is a particular specification of the type and arrangement of the primitives while the phenotype is the designed artifact as a whole. The genotype can be thought of as a program which details how to build the phenotypic artifact. Using this simple analogy, a GA used for design can be considered a manipulator. It manipulates low-level ``tools,'' playing with their arrangements, until it finds the required structure. Encoding therefore consists of finding a set of low-level tools for the GA to manipulate. The number of possible codings to choose from may be very large and it is fortunate that GAs are robust and work quite well on arbitrarily chosen encodings. However in addition, the following two principles are often used (Goldberg, 1989).
However, in the kind of spaces often encountered in design, a designer may not know whether either principle of GA coding is being followed. The mapping from genotype to phenotype is now much more complex. To get an idea of this complexity, compare the structure of an eye (a design phenotype) with a point in the search space (a phenotype in function optimization) Interdependence in phenotypic space may not be reflected in the genotype, unless it is very carefully encoded, and may cause a GA to be mislead because it violates the first principle. Epistasis, or interrelationships among components, in phenotypic structures therefore plays an important part in determining the suitability of an encoding for design.
At first glance, the second principle may seem to be much simpler to follow.
Since digital computers ultimately represent all objects in bits and bytes, the
problem reduces to making sure that genetic operators work on this binary
representation. In fact, the efficiency of bit operations in digital computers
is motivation for using a binary representation for genotypes. However, the
problem is to arrange for such an encoding to simultaneously follow the first
principle. Our intuition about design spaces may not translate into an
understanding of the binary encoded spaces that GAs thrive on.
Chapter gives an example of this type of problem, suggests
a solution, and presents favorable empirical evidence in support.
Evaluating a design measures performance relative to predetermined criteria. If the criteria are well defined, a scalar or vector value can be assigned to a candidate design and compared with others. On the other hand if the problem is ill-structured and the criteria are not well defined, precision may decrease, leading to fuzzy quantization. This may knock some paradigms out of contention, but GAs are remarkably resilient. When using a distributed selection mechanism, such as tournament selection, all that is needed from the evaluation function is a partial ordering on the generated population of design alternatives. If the performance criteria are ill-defined, an interacting designer can bring aesthetic and/or other judgments into the evaluation process and need only compare pairs of candidate solutions indicating which is better.
For example, consider the problem of constructing a composite of a criminal's face by an eyewitness to the crime. Caldwell and Johnston describe a system that uses a genetic algorithm to rapidly search through a search space containing over 34 billion possible facial composites [Caldwell and Johnston, 1991]. The eyewitness interactively and subjectively establishes the measure of fitness used to guide search. The algorithm combines building blocks made up of five basic features. The type and position of the forehead, the eyes and their separation, and the shape and position of nose, mouth and chin, respectively. In their example, just 10 generations suffice to generate a composite that is remarkably similar to the criminal.
The genetic algorithm is also quite resistant to noise in the evaluation process and noisy judgments are processed in useful ways [DeJong, 1975]. In all cases, once a partial ordering is available, selection can prune the search and concentrate on a computationally tractable subset of the space.
This section uses a floorplanning problem [Radford and Gero, 1988] to ground the
issues discussed so far. Consider the apartment floorplan shown in
figure . The problem is to find the length and width of each room that
will minimize the cost of the apartment, subject to some constraints. The cost
for each room in this case is the area except for the cost of the kitchen and
bathroom, whose costs are twice their respective areas. The constraints are:
Further, there must be a space -- 3.0 units -- for a doorway in the walls connecting bed2 and bed3 to the hall, and all rooms are rectangular (as is the entire plan).
Figure: Dimensionless floor plan of a three bedroom apartment
This design problem is a nonlinear optimization problem and can be formulated mathematically as follows. Let length be the horizontal dimension and width the vertical dimension, then the variables are given in the table below.
Although at first glance there appear to be fourteen variables, one each for the length and width of each room, analysis of the problem reveals that some of the variables can be computed from others. For example the width of the hall is the width of the living room minus the width of the bathroom.
The design task is to minimize the cost of the apartment, that is, minimize
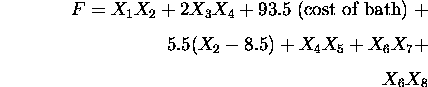
subject to the following constraints:
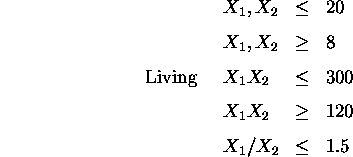
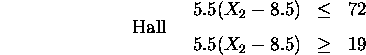
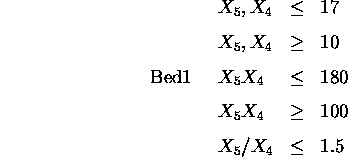
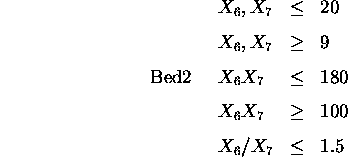
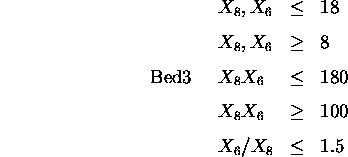
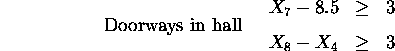
In addition the whole plan is rectangular therefore:
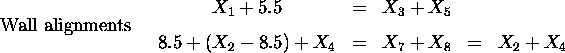
To use a genetic algorithm on this problem these constraints must be
incorporated in the encoding or the objective function F, and the design
variables ( 
... 
) have to be represented in a form suitable for a
GA. That is, each variable must be encoded in a bit string and the concatenated
string of all variables forms the genotype. Since the minimum and maximum value
of each variable is given, only the range (the difference between the maximum
and minimum values) needs to be represented. The maximum range is 12 and as
an accuracy of about 0.5 units is sufficient, 11 bits are used to encode
the variables with a range of 12 and 10 bits for the rest. 11 bits can be
used to represent values from 0 to 2048 and must be mapped to the values
from 0 to 12, thus if 
represents the binary encoded value of the
first variable's ( 's) range, the length of the living room can be computed
through
where Min 
, the minimum length of the living room. The genetic
algorithm therefore codes for the range from 0 through 12 in increments of
12.0/20.48. Increasing the number of bits for by 1 would result in a
precision of 12/40.96. In this way the constraints on the maximum and minimum
lengths and widths of rooms are assimilated in the encoding.
Violation of constraints on area, proportion, door and wall alignments take the form of penalties which increase the total cost. Thus the function to be minimized -- the objective or evaluation function -- becomes:
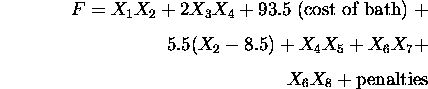
A genetic algorithm can now work on the encoded design problem. Starting with an initial random population of solutions encoded as described above, selection evaluates candidate solutions, while crossover and mutation synthesize new solutions. The minimum cost found by sequential linear programming, an optimization technique that first converts the problem to a linear one and then solves it, is 715.98 units and this solution violates some of the constraints. In experiments with a population size of 30, crossover probability of 0.9, and a mutation probability of 0.01, genetic algorithms find solutions that have costs from 689.30 to 752.92 with various degrees and types of constraint violations. This allows an engineer or architect to choose from among the solutions, produced in less then a minute on a work station.
This chapter has illustrated how genetic algorithms model the design process. They mirror the three stage model of analysis, synthesis and evaluation searching through a large space of possible designs for near-optimal structures. Noisy environments, perhaps a side effect of ill-structured problems, do not cause major problems. In interactive systems where human designers can help evaluate ill-defined criteria (beauty, elegance etc.), GAs only need pairwise comparisons of candidate solutions and do not need other more time consuming evaluations. Finally, a floorplanning problem was used to illustrate the issues involved in analyzing and encoding a problem for a genetic algorithm.
Nevertheless, there are problems. Usually, domain information resides in the evaluation function, but performance of a GA depends on the suitability of the encoding. That is, whether it follows the two principles of GA encodings. Domain knowledge also plays a large part in deciding if a particular encoding is appropriate. But given the same problem and encoding, when is a genetic algorithm expected to perform better than other blind search algorithms? Next, whatever the underlying knowledge-base and its representation, there is first the problem of encoding this domain knowledge for a GA. Third, although GAs may be expected to invent new designs, analysis of why the design works and what are its strong and weak points is difficult. Finally, the time to convergence -- the time that a GA should run -- must be bounded before a computational tool can be advanced.
