'Life is very strange' said Jeremy. 'Compared to what?' replied the spider. -Anon
This chapter compares genetic algorithms with other search algorithms. It defines a class of search spaces which are easy for genetic algorithms and hard for stochastic hill-climbers. The defined spaces require genetic recombination for successful search and are partially deceptive. A deceptive space for a search algorithm leads the algorithm away from the global optimum and towards a local optimum. Problems where tradeoffs need to be made subsume spaces with these properties. Results comparing a genetic algorithm without crossover against one with two-point crossover support these claims. Further, a genetic algorithm using pareto optimality for selection outperforms both. In problems with more than one criterion to be optimized, pareto optimality provides a way to compare solutions without the need to combine the criteria into a single fitness measure. These results provide insight into the kind of spaces where recombination is necessary, suggesting further study of properties of such spaces, and when to expect genetic algorithms to outperform others.
Recombination plays a central role in genetic algorithms and constitutes one of the major differences between GAs and other applicable algorithms. Therefore, the answer to the question of whether a search space is particularly suited to a genetic algorithm hinges on the power of recombination in generating an appropriate search bias. This chapter defines one class of spaces that requires genetic recombination for successful search. The class includes problems where a particular kind of tradeoff exists and is exemplified by design problems in engineering and architecture.
Recent work on GA-easy and ``royal-road'' functions suggests that it is not easy to find spaces where GAs emerge a clear winner when compared with a stochastic hill-climber (SHC) or a population of stochastic hill-climbers [Wilson, 1991, Mitchell and Forrest, 1993]. The work suggests that it is not enough that optimal lower order schemas combine to form optimal higher order schemas. Hill-climbers often solve such problems in a smaller number of function evaluations than a genetic algorithm. Instead, research on deception provides insight into the kinds of spaces that are deceptive [Goldberg, 1989a] for SHCs or a population of SHCs and that are relatively easy for genetic algorithms. Identifying properties of spaces that are easy for genetic algorithms and hard for stochastic hill-climbers should provide insight into the inner workings of a GA and aid in the practical selection of search algorithms.
The next section defines the model of a stochastic hill-climber used in this chapter. Then a problem that is partially deceptive and needs recombination to overcome deception is designed. Spaces with structure similar to the problem defined in section three may be found in multicriteria optimization. Pareto optimality, used to compare multicriteria solutions, is defined in section four and used in selecting candidates for recombination in a genetic algorithm. Empirical evidence in section five compares performance on the problem type defined in section three.
The model of a classical genetic algorithm in this chapter assumes proportional
selection, two-point crossover and a mutation operator that complements a bit
at a randomly selected position. Proportional selection selects a candidate for
reproduction with probability proportional to the fitness of the candidate.
That is, if 
is the fitness of individual i, its probability of
selection is
where N is the population size. Two point crossover is like one-point
crossover (figure 
), except that two points are randomly chosen
and the substring defined by those points exchanged to produce offspring. For
experimental purposes a population of stochastic hill-climbers is a genetic
algorithm without crossover. In this chapter ``hill-climber'' and ``stochastic
hill-climber'' are used interchangeably and problems are cast as maximization
problems in hamming space, eliding the issue of encoding.
A genetic algorithm without crossover and only mutation can be likened to an
Evolution Strategy [Bäck et al., 1991], albeit a simple one with a
nonvarying mutation rate and random bias. A GA without crossover is a
stochastic hill-climber and, depending on the rate of mutation, can make jumps
of varying sizes through the search space. Being population-based and
stochastic, it makes fewer assumptions about the search space, and as such is
more robust and harder to deceive than the bit-setting optimization and
steepest-ascent optimization algorithms defined in Wilson's paper
[Wilson, 1991]. A bit-setting optimization algorithm assumes that a point in
the search space is represented by a bit string S of length l. The
algorithm flips each bit, remembering the settings that led to improvements.
The solution 
consists of the better settings of each bit.
Steepest-ascent optimization accepts as the starting point for
iterating bit-setting optimization. This continues until no improvements can be
made.
Although there is debate in genetics as to the evolutionary viability of crossover in nature, it suffices to note that crossover does exist in biological systems. In genetic algorithms, Holland's schema theorem emphasizes the importance of recombination and provides insight into the mechanics of a GA [Holland, 1975]. Recombination is the key difference between the genetic algorithm and the hill-climbers defined above. Recombination allows large, structured jumps in the search space. In other words, it facilitates combination of low-order building blocks to form higher-order building blocks, if they exist. The type of combinations facilitated depends on the crossover operator and population distribution. In a random population of strings (encoded points), large jumps in the search space are possible. However, the size of jumps due to crossover in a GA depends on the average hamming distance between members of the population (hamming average) or the degree of convergence of the population. The hamming distance between two binary strings of equal length is the number of corresponding positions that differ. For example, the hamming distance between 1011 and 0010 is 2 since the bits in the first and last positions differ. As the population converges, the usual and corresponding decrease in hamming average of the population leads to a decrease in maximum jump size and exploration of a correspondingly smaller neighborhood. But this kind of neighborhood exploration can be carried out by a GA with mutation only, that is, a stochastic hill-climber.
During the early stages of GA processing, large jumps, combinations of building blocks that are hamming dissimilar, are more probable since the hamming distance between possible mates is higher. The GA should search effectively in spaces where such combinations of building blocks lead toward higher-order optimal schemas. But at this early stage, not only is the variance in estimated fitnesses of schemas high, but there may be enough diversity in a population of hill-climbers to stumble on the correct higher-order schema. Both the order of early building blocks and diversity of the population need to be considered in analyzing recombination.
The discussion above implies that for recombination to be effective and hill-climbing ineffective, a GA needs to be able to make large, useful, structured jumps through recombination even after partial convergence.
Consider the function shown in figure .
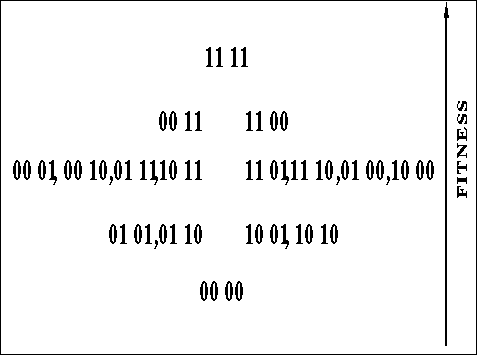
Figure: A hill-climbing deceptive function that should be easy for GAs
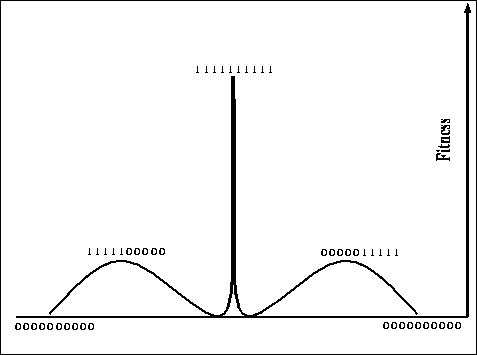
Figure: An alternate view of a hill-climbing deceptive space that should
be easy for GAs (10 bits)
For this four-bit function, the global optimum is at 1111, but there are two
hill-climbing deceptive optima at 0011 and 1100, the global optimum is 2
bits away from the suboptima. Figure gives another rough, but
perhaps more intuitive, view of a space that should be easy for a GA.
Broadening the base of the peak in figure makes the function easier
on hill-climbers and genetic algorithms alike. The function in
figure can be specified for an l length string as follows: let
be the number of ones on the right half of the string (l/2 bits), 
be the number of ones on the left half of the string. Using 
to
denote the absolute-value function, and p the size of the base of the peak,
Intuitively, counting from one side (left or right), fitness increases as the number of 1's increases until the halfway point of the string, after this point, fitness decreases as the number of 1's increases until reaching the area near the global optimum. Here the fitness increases sharply, peaking at the global optimum. The squaring of the values near the peak tries to ensure that once found by a classical genetic algorithm, the peak will not be lost easily.
For sufficiently large l this type of function is deceptive for a SHC or
population of SHCs since for a string of length l, once a stochastic
hill-climber reaches a deceptive optimum, it will have to simultaneously set
all the remaining l/2 (approximating to within p bits) bits to 1 to
attain the global optimum. Setting fewer than l/2 bits decreases fitness.
The probability of simultaneously setting l/2 bits to 1 decreases
exponentially with l, thus making it hard on a SHC or a population of SHCs
for sufficiently large l. Using this chapter's model of a stochastic
hill-climber with mutation probability 
, after reaching the suboptima, the
probability of setting l/2 bits is: the probability that l/2 incorrect bits
are flipped, multiplied by the probability that the correctly set bits are not
flipped
Now consider the power of recombination. Once a genetic algorithm reaches the hill-climbing deceptive optima, crossover can produce the global optimum in one operation, assuming that the population contains representatives of both suboptima. Genetic operators that are conducive to maintaining stable subpopulations at the peaks of a multimodal function are called niching operators (see [Deb and Goldberg, 1989] for a survey of niching operators). Niching operators can be used to provide representatives at the suboptima as long as these operators do not entail mating restrictions which may then not allow the algorithm to find the global optimum.
Next, consider whether this type of space may be found in normal application domains. In many areas of engineering, a problem is usually stated in terms of multiobjective (or multicriteria) optimization, and the function above can be easily and naturally stated as a two-objective optimization problem. This dissertation suggests that multicriteria optimization problems may provide fertile ground for finding search spaces in which genetic algorithms do better than other blind search algorithms. However, multicriteria optimization raises a point. The issue for the algorithms presented earlier is that, in general, it is difficult to combine multiple measures into a single fitness in a reasonable way without making assumptions about the relationships among the criteria. Unfortunately, a single fitness measure is the usual feedback for genetic algorithms and for the niching methods in [Deb and Goldberg, 1989]. For example, consider designing a beam section where the objectives are to maximize the moment of inertia and minimize the perimeter. Minimizing the perimeter usually decreases the moment of inertia and maximizing the moment of inertia increases the perimeter, resulting in a tradeoff [Gero et al., 1993]. Combining the two criteria into a single measure makes no sense unless the relationship between the two is already known. Fortunately, the concept of pareto optimality allows us to do this reasonably and, as will be seen, provides a ready-made niching mechanism, killing two birds with one stone.
Pareto optimality operates on the principle of nondominance of solutions. An
n criteria solution 
with values 
dominates
with values 
if
The set of pareto optimal solutions, the pareto-optimal set, is the set of
non-dominated solutions. Figure shows the pareto-optimal set for a
two-criteria problem. An axis represents values for a particular criterion. The
coordinates of each point (solution) denote the values of their respective
criterion. X's in the figure represent dominated points. The O's represent
non-dominated points that belong in the pareto-optimal set.
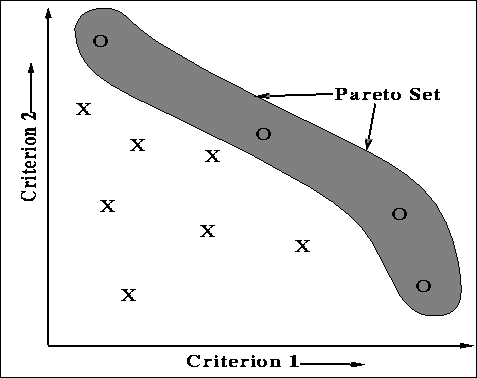
Figure: A graphical representation of solution points on a two-criteria
optimization problem. The points within the shaded area represent the pareto
optimal set of solutions.
Considering the maximal value along each criteria to be one of our
hill-climbing deceptive optima, there is a correspondence between the function
defined in section 2 and multicriteria optimization problems. If a central
peak (global optimum) exists, as in figure , then recombination
should find it, if both suboptima are represented in the population.
Incorporating pareto optimality into the selection mechanism of a genetic
algorithm facilitates the maintenance of stable subpopulations representing the
suboptima.
A variant of binary tournament selection is used to incorporate pareto optimality in the genetic algorithm. When using this variant of binary tournament selection, the algorithm selects two individuals at random from the current population, mates them, and produces the pareto-optimal set of the parents and offspring. Two random individuals from this pareto-optimal set form part of the next population. The procedure repeats until the new population fills up, thus becoming the next current population. This method with a tournament size of 2 is computationally inexpensive since only 4 solutions compete at a time.
The genetic algorithm with pareto-optimal selection (pareto-optimal GA) is used
to attack the problem in section . First, the problem is split
into two, corresponding to the two additive terms in equation . Cast
as a 2 criteria optimization problem, the first criterion is
where stands for the number of 1's in one half of the string and
the number of 1's in the other half of the string. The second criterion 
then becomes
The point of decomposing the original problem into a two-criteria problem is not to suggest that functions in general can be decomposed to form multicriteria problems. Rather, the argument is that many design problems are best posed as multicriteria optimization problems and thus provide search spaces that may be easy for genetic algorithms.
This section compares the number of times the optimum is found by a GA without crossover, a classical GA with two-point crossover (CGA) and a pareto-optimal GA with two-point crossover. The population size in all experiments was 30 and the results were averaged over 11 runs of the algorithm with different random seeds. The GA with mutation ran with mutation probability from 0.01 to 0.10 in increments of 0.01 and the best results used. The probability of crossover was 0.8 and the mutation rate 0.02 for the other two algorithms.
Figures and compare the maximum fitness over
time for the three algorithms. The algorithms ran for 200 generations or
6000 function evaluations. The string length was 30, the parameter p in
the definition of the function was set to 2 to produce figure
and to 4 to produce figure . The difference in performance of
the pareto-optimal GA provides empirical support for the importance of
recombination and the niching effect of pareto-optimal selection. As expected
the width of the peak affects performance, with wider peaks allowing the GA
with two-point crossover to perform significantly better than the stochastic
hill-climber. The plot for the pareto-optimal GA shows the average fitness for
only one of the two criteria, hence the low (about 1/2 the value of the other
two plots) initial values.
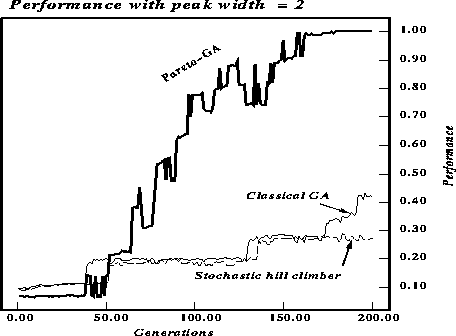
Figure: Performance comparison for string length 30. The peak width is 2.
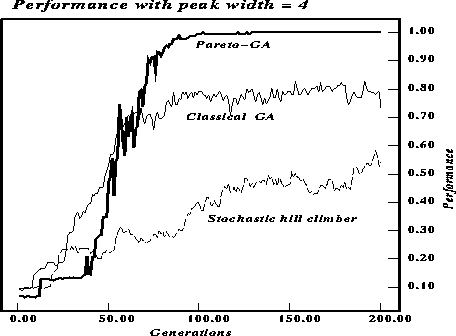
Figure: Performance comparison for string length 30 but with peak width 4.
Table compares the percentage of times the algorithms found the
optima for strings of length 20, 30, 40 and 50 for peaks of width 1,
2, 3 and 4. In the table, peak size is given in column 2, PGA is the
pareto-optimal GA while CGA is the GA with two-point crossover and PSHC is the
GA with no crossover -- a population of stochastic hill-climbers.
Table depicts the same information but for wider peaks.
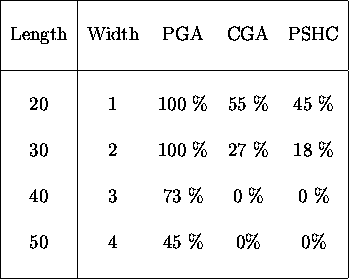
Table: Comparing the number of times the optimum was found in
200 generations for narrow peaks.
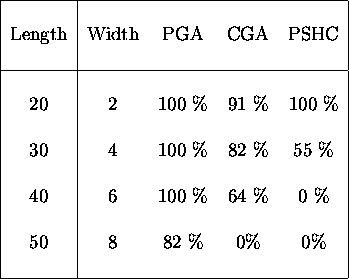
Table: Comparing the number of times the optimum was found in
200 generations for broader peaks.
For table , statistical testing using a 
test of
significance for comparing proportions indicates that the PGA is significantly
better at a confidence level greater than 95% for the length-20 problem and
a significance level greater than 
for the others. The difference in
performance of the CGA and PSHC is not statistically significant for any of the
problems in this table. Table shows the significance and
confidence levels for the data in table . Comparing performance
using date for the wider peaks given in table , the test
indicates that the differences in performance between the PGA and CGA and
between the CGA and PSHC on the 30 bit problem are statistically significant.
The confidence level is greater than 
. On the 40 and 50 bit problems
the pareto-optimal GA significantly outperforms the other algorithms.
Table: Statistical Significance of differences in
performance according to the test of significance. Confidence levels
are in parenthesis.
These results strongly indicate that a pareto-optimal GA is more likely to find
the optimum on problems of this type, followed by a GA with crossover. The
stochastic hill-climber appears least likely to find the optimum and in this
case had less than a 
chance, even on the smaller length-20 problem
when the peak was narrow. Wider peaks help the hill-climber for small problems
(length 20, peak width 2) but as the problem size increases, the
hill-climber's performance deteriorates to become worse than even a classical
GA. In all cases, the pareto-optimal GA does as well as, or better than, the
other two algorithms.
A preliminary analysis assumes that the algorithms need to reach the local
optima to be able to jump to the global optimum. For the function type defined
in this chapter, as the length of the deceptive basin between a local optimum
and the global optimum decreases, hill-climbers should perform better. A
break-even point for a function shaped like the one in figure
occurs when the chances of reaching the global optimum from one of the local
optima become greater than 1/2. From the earlier analysis the probability
that a stochastic hill-climber reaches the global optimum is
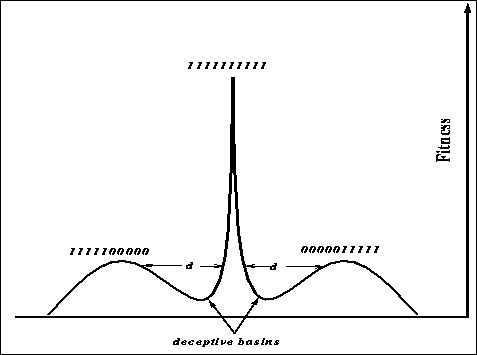
Figure: The shape easier for GAs and harder for hill-climbers, d denotes the
size of the deceptive basin.
where is the probability of mutation and l the length of the string.
Let d stand for the length of the deceptive basin (l/2 is the length of the
deceptive basin above). Figure is a copy of figure but
with the deceptive basin size d clearly marked. Plotting the function for
various values of and d results in figure .
Figure: The vertical axis indicates the probability of finding the global
optimum in terms of mutation rate ( ) and length of deceptive basin (d).
The plot (figure ) indicates that the length of the deceptive
basin plays a major part in determining success for a stochastic hill-climber.
Only for small values of d are the chances of finding the optimum appreciable
over a range of mutation values. For a genetic algorithm using one-point
crossover, the probability that the global optimum is found assuming equally
fit local optima is roughly the probability that the mates chosen represent the
two local optima, multiplied by the probability that crossover produces the
global optimum. Assuming that the genetic algorithm population only contains
representatives of the local optima in equal proportions, the probability of
finding the global optimum is 
. This simplified analysis
assumes that the algorithms need to reach the local optima to be able to jump
to the global optimum. The assumption is not strictly true. Analysis becomes
much more complex, depending on the detailed behavior of the objective
function, when disallowing this assumption. However, macroscopic behavior, like
the importance of deceptive basin length (d) is predictable.
Design problems are often formulated as multiobjective or multicriteria optimization problems. In many cases such problems involve tradeoffs among possibly conflicting criteria. Spaces where recombination of two or more single criterion optima leads toward a global optimum, with a deceptive basin in between to trap hill-climbers, are well suited for genetic algorithms especially when using pareto optimality in their selection process. Pareto-optimal selection appears to provide the necessary niches until recombination produces the global optimum. This chapter defined a problem in hamming space with these properties and empirically compared the performance of a classical GA with two-point crossover to that of a stochastic hill-climber (a GA without crossover), and a GA with pareto-optimal selection. The GA with pareto-optimal selection always found the optimum more often than the others, while the classical GA usually did better than the stochastic hill-climber. This evidence suggests a closer look at the spaces defined in this chapter for function encoding combinations that are relatively easy for genetic algorithms and hard for hill-climbing methods.
Pareto-optimal selection also eliminates the need to combine disparate criteria into a single fitness as is usual in genetic algorithms. The method described in this chapter is distributable and computationally less expensive compared to other suggested methods for incorporating pareto optimality [Goldberg, 1989b]. Exploring niche formation with pareto-optimal selection remains an interesting area for further research.
This chapter did not consider encodings since all problems were cast as optimization problems in hamming space. However, encoding a problem for a genetic algorithm is an important issue, with the biases generated by an encoding playing a significant part in performance. The next chapter attacks this problem.
