Everyone designs who devises courses of action aimed at changing existing situations into preferred ones.-H. A. Simon. The Sciences of the Artificial, MIT Press, 1969.
Design is a fundamental, purposeful, pervasive, and ubiquitous activity. As Simon pointed out, anyone who formulates programs of action to change an existing state to a preferred one is solving design problems [Simon, 1969]. Planning, scheduling, circuit design, VLSI layout, architecture, and most branches of engineering are, or can be cast as, design problems. Any useful tool that helps the design process would be widely applicable. Current tools are based on a knowledge intensive view of the design process. Techniques like expert systems and case-based reasoning, apart from problems with the acquisition of knowledge, suffer from a basic flaw: they fail on new and/or poorly-understood application domains, where there is insufficient knowledge to proceed.
Genetic algorithms (GAs) are randomized parallel search algorithms that model natural selection, the process of evolution. Over time, natural selection has produced a wide range of robust structures (life forms) that efficiently perform a broad range of functions. The success of natural selection on earth provides an existence proof of the viability of an evolutionary process as a model for design. Like natural selection, GAs are a robust search method requiring little information to search effectively in large, poorly-understood spaces.
In this context, the central claim of the thesis is
Genetic algorithms provide a computational tool for the design problem: ``Given a function and a target technology to work within, design an artifact that performs the function subject to constraints.''
Although genetic algorithms have been used in engineering problems, there are reasons why designers are reluctant to embrace GAs. Representation problems are one reason familiar to artificial intelligence researchers. There was no bound on the time to convergence until recently [Louis and Rawlins, 1993b]. This thesis identifies and overcomes four basic problems in establishing genetic algorithms as a computational tool for design.
The current chapter expands on the definition of design, the nature of design problems, and casts design as search through a state space. After identifying the questions addressed in this thesis, the chapter ends by providing an overview of the structure of this dissertation.
Design's pervasive nature makes it difficult to find a concise, comprehensive, and well-accepted definition. Attempts at defining design usually reflect the bias of the author and range from the mundane to the theoretical. Dasgupta's book provides some historical as well as modern attempts at such definitions [Dasgupta, 1991]. More recently, Chris Tong and Duvvuru Sriram advance a fairly comprehensive definition and describe design as ``the process of constructing a description of an artifact that satisfies a (possibly informal) functional specification, meets certain performance criteria and resource limitations, is realizable in a given target technology, and satisfies criteria such as simplicity, testability, manufacturability, reusability, etc.'' [Tong and Sriram, 1992b].
The various definitions agree, however, that design is concerned with the
mapping of a specified function onto a structure or description of a
structure.
Usually, the
designed structure also satisfies performance, resource, and other pragmatic
constraints. In addition, most design theorists agree that the goal of design
is to purposefully initiate change in some aspect of the
world [Simon, 1969, Tong and Sriram, 1992b]. Unlike theories of the natural sciences,
design is concerned with construction of artifacts and the purposeful effecting
of change.
The main reason for the difficulty of design tasks lies in the complexity of the mapping between function and structure. The specified function may be very complex and/or it may have to be realized using complex arrangements of a large number of interacting parts. Typically, the behavior of each component is well known, and the difficulty lies in predicting how an assemblage of such components will behave. Additional non-functional criteria and constraints complicate the design problem even further.
The type of structure synthesized can be used to distinguish design tasks [Tong and Sriram, 1992b]. In structure synthesis, the design is constructed from the composition of primitive parts into a structure that performs a specified function. Constructing a parity-checker circuit from logic gates is an example of this type of task. This may not be optimization, but rather, as noted by Simon, it may be a satisficing task, in that a designer searches for a circuit that checks parity, not an optimal circuit [Simon, 1969].
In structure-configuration tasks, the design is a configuration of parts of pre-determined type and connectors of pre-determined type. For example, in floorplanning, the problem is to design a configuration of rooms and doors to fit in a given area, along with the values of room and door parameters.
Lastly, in parameter-instantiation tasks, the problem is to find the values of parameters such that a particular design can be instantiated.
In all the cases above, optimization plays a role, since there is usually a cost associated with each design. Minimizing this cost can be part of the original design task or it may be a separate task.
Casting design as a search problem, a formulation with a well-established heritage in artificial intelligence research, a design process searches through a state space of possible structures for one or more structures that perform a specified function. Points in the state space represent candidate designs, and one or more of these points defines a goal state representing a design that meets specifications.
In search there is a tradeoff between flexibility -- applicability in different domains, and speed -- the number of candidate designs searched through before finding the correct one. Current design systems tend to depend on domain-specific knowledge and favor speed over flexibility. Most are so brittle that they fail completely when domain knowledge is scarce. Genetic algorithms, on the other hand, can make do with little domain knowledge, make few assumptions about the search space, and use domain-independent operators for generating candidate points in a state space.
If there is sufficient knowledge about a problem domain, there is no need to search for a solution. However, if there is insufficient knowledge about a domain to arrive directly at a solution, then if there is at least enough information to delineate an area within which a solution is expected to be found, a search method can be used to hunt for a solution within the delineated area.
This thesis is concerned with design problems that do not lend themselves to a direct solution but that can be cast as search problems within a space of possible solutions.
Search algorithms typically have two components corresponding to the tradeoff between speed and flexibility. They balance exploration of the search space with exploitation of areas of the space. Exploration points out new areas to search in, while exploitation concentrates search in a particular area. The need for a balance arises because unchecked exploration leads to wasted time in unpromising areas, while severe exploitation may miss the correct solution by concentrating on too small an area. That is, too much exploration means too much time, and too much exploitation means that the correct solution may not be found. On the other hand, if there is not enough exploration, the correct solution may not be generated while insufficient exploitation may take too long. Striking a good balance between exploration and exploitation is therefore critical for a search algorithm.
Wasting time in unpromising areas of the search space may seem a small price to pay for finding the correct solution. Unfortunately, the size of the search spaces that arise in design domains is often so large that a human lifetime is short compared to the time needed by the fastest supercomputers to look at a significant fraction of the space. This is why random and/or exhaustive search (RES) is infeasible: it explores too much. On the other hand, RES works equally well across all search spaces, since it makes the fewest assumptions about exploitable properties of the search space. It assumes that a minimal amount of knowledge is available -- enough to know when to stop. Put another way, RES needs and uses minimal information about the search space to work equally well across a variety of spaces.
At the other extreme are algorithms that do no exploration and have knowledge available to solve the problem quickly and directly. These algorithms make strong assumptions about the search space and sufficient exploitable information is available to avoid searching. However, because these strong assumptions do not usually hold across domains (search spaces), these algorithms work only on the particular space they were designed for and do miserably on others.
In between these extremes of random and/or exhaustive search and no search, every other search algorithm makes assumptions of varying kinds about search spaces. These assumptions correspond to knowledge about the space and may be correct, incorrect, or misleading, implicit or explicit, and known or unknown, when used for searching a particular space. This knowledge is exploited to guide exploration, speeding up search by generating a search bias manifested in the set of generated solutions.
Genetic algorithms belong to a class of algorithms, called blind search algorithms, which make the assumption that there is enough knowledge to compare two solutions and tell which is better [Rawlins, 1991]. Genetic algorithms are the search method of choice for this dissertation.
A Genetic Algorithm (GA) is a randomized parallel search method modeled on evolution. GAs are being applied to a variety of problems and becoming an important tool in machine learning and function optimization. They have already been used in the preliminary design of aircraft engine turbines and, more recently, in protein structure prediction [Powell et al., 1989, Le Grand and Merz Jr., 1993]. Goldberg's book gives a list of application areas [Goldberg, 1989b].
Intuitively, genetic algorithms can be understood in terms of differences with
other search methods that can be applied in the same situation. Consider the
problem of finding the correct combination for opening a thirty-digit
combination lock (designing a key). One possible algorithm is random and/or
exhaustive search. In this case the only information used by the algorithm is
whether or not the currently generated combination is the correct one. With
this algorithm the chances of success -- finding the correct combination --
are better than 1/2 only after the generation of 
combinations.
This is a very large number. In fact, if RES generates a combination every
nanosecond, it would take more than the age of the earth before success is more
than 
probable.
If, in addition to whether the current combination is correct, more information is available, a search algorithm could use this information to increase efficiency. Hill-climbing or gradient-descent algorithms, when given information about which of two generated combinations is ``closer'' to the correct combination, make use of this additional, directional information to speed up the search. The hill-climbing analogy considers the search space as a landscape through which a search algorithm moves towards the highest point, where height corresponds to ``closeness'' to the optimum. However, a hill-climber can be trapped on a hill that is not a global optimum but a local optimum. In other words, if the search landscape is rugged with a lot of hills (local optima), the algorithm could climb the nearest hill and find that any further movement decreases height and thus remain trapped on this hill, whereas the highest point (global optimum) is actually on another taller hill.
A population of hill-climbers is more robust. Trapping a large number of hill-climbers, working independently on the same problem, is less probable than trapping just one hill-climber.
Genetic algorithms are more than a population of hill-climbers. In addition to having a population of individuals that hill-climb, genetic algorithms allow the exchange of information among individual hill-climbers in generating combinations that are ever closer to the correct one. Genetic algorithms exemplify the maxim: ``Two heads are better than one'' and can be considered a population of information-exchanging hill-climbers.
When used in design, a GA encodes a candidate design in a binary
string.
A randomly generated set of such strings forms the initial population from
which the GA starts it search. Three basic genetic operators: selection,
crossover, and mutation guide this search. The genetic search process is
iterative: evaluating, selecting, and recombining strings in the population
during each iteration (generation) until reaching some termination condition.
The basic algorithm, where P(t) is the population of strings at generation
t, is given below.
t = 0initialize P(t)
evaluate P(t)
while (termination condition not satisfied) do
begin
select P(t+1) from P(t)
recombine P(t+1)
evaluate P(t+1)
t = t+1
end
Evaluation of each string is based on a fitness function that is
problem-dependent. It determines which of two candidate solutions is better
(figure 
).
Figure: Evaluating individuals determines which is better.
This corresponds to the environmental determination of survivability in natural
selection. Selection of a string, which represents a point in the search space,
depends on the string's fitness relative to that of other strings in the
population. It probabilistically culls from the population those points that
have relatively low fitness (figure ).
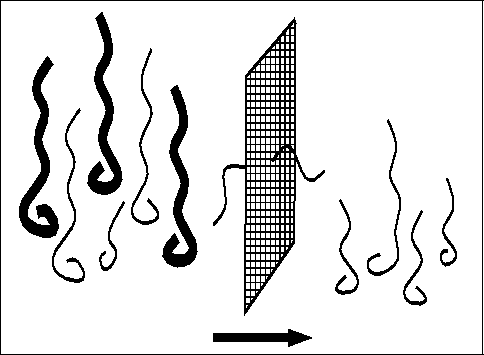
Figure: Selection acts as a sieve, selecting better individuals to continue.
Mutation and crossover imitate sexual reproduction. Mutation, as in natural
systems, is a very low probability operator and just flips a specific bit.
Crossover in contrast is applied with high probability. It is a randomized yet
structured operator that allows information exchange between points. Simple
crossover is implemented by choosing a random point in the selected pair of
strings and exchanging the substrings defined by that point. Figure
shows how crossover mixes information from two parent strings, producing
offspring made up of parts from both parents. Note that this operator which
does no table lookups or backtracking, is very efficient because of its
simplicity.
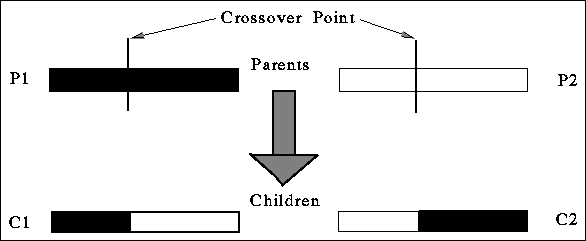
Figure: Crossover of the two parents P1 and P2 produces the two children C1
and C2. Each child consists of parts from both parents which leads to
information exchange.
Selection probabilistically filters out designs that perform poorly, choosing high performance designs to concentrate on or exploit. Crossover and mutation, through string operations, generate new designs for exploration. Thus genetic algorithms only require two elements: 1) an encoding of candidate structures (solutions), and 2) a method of evaluating the relative performance of candidate structures. Given an initial population of elements, GAs use the feedback from the evaluation process to select fitter designs, generating new designs through recombination of parts of selected designs, eventually converging to a population of high performance designs. Since GAs only require feedback on the relative performance of candidate designs to guide search, they are applicable in any design task that can provide this information. In other words, given a function to perform, a genetic algorithm only needs to know which of a pair of candidate designs is ``closer'' to performing the function. And even this information need not be perfect but can be subject to noise and misdirection to some extent. This thesis is only concerned with such design problems.
However, there are unresolved problems in using genetic algorithms for design. First, although genetic algorithms allow sharing information among hill-climbers, are there search spaces where this sharing leads to better performance? Second, since genetic algorithms work with an encoding of the problem, what kind of biases can be expected to be introduced by the encoding and can the genetic algorithm surmount unfavorable encoding biases? Third, genetic algorithms should be applied in knowledge lean domains where the solutions that are found tend to be difficult to understand. The question is, what kind of analysis is possible of genetic algorithm designs? Finally, given a problem, how long should a designer run a genetic algorithm on it?
The dissertation addresses each of these problems in turn, using design examples from circuit design, floorplanning and function optimization.
Although design encompasses a lot of fields, this thesis is most concerned with work that has been done at the nexus of engineering, architecture, and artificial intelligence. Perhaps the closest piece of research connected to this dissertation is in using genetic algorithms to design computer programs.
John Koza uses genetic algorithms to evolve programs in the LISP programming language, illustrating the use of genetic algorithms in the task of program design [Koza, 1993]. The work presented in this thesis is however, qualitatively different. This dissertation develops tools and methods, and addresses questions and problems, that can arise in using genetic algorithms in any applicable design task and thus attempts to address more foundational issues.
Knowledge-based systems for design depend on domain knowledge to accomplish design tasks. A description of the state of the art in engineering design can be found in [Tong and Sriram, 1992a]. Systems that use a combination of techniques also exist. Such integrated design environments use a variety of tools to structure and attack design problems. ``Engineous'' is a system that includes genetic algorithms in its toolbox to uncover unconventional designs when needed [Tong et al., 1992, Powell et al., 1989]. The work in this thesis should help improve the construction, use and applicability of such genetic algorithm tools.
Innovation and creativity are often associated with design processes.
Chapter explains in what sense genetic algorithms can be
considered innovative. Other approaches to innovative engineering design can be
found in [Mostow et al., 1992, Huhns and Acosta, 1992, Sycara and Navinchandra, 1992, Goel and Chandresekaran, 1992, Ulrich and Seering, 1992, Tong, 1992]. These approaches include
case-based reasoning, structural mutation, and innovation through the
combination of multiple knowledge sources. Lenat's work on heuristics and
meta-heuristics can also be considered as an innovative approach to the design
of effective strategies [Lenat, 1983].
Modeling the creative aspects of a design process is addressed in [Gero, 1992, McGraw, 1992]. The work in [Gero, 1992] seeks to define and model the creative aspects of a design task. Letter Spirit, the project described in [McGraw, 1992], attempts to model central aspects of human high-level perception and creativity on a computer, in the domain of artistic letter-design. This dissertation does not address creativity.
Chapter introduces natural selection and genetic algorithm
theory, fleshing out the problems identified above. Although search is the
model used in this thesis, the chapter also illustrates the close mapping
between genetic algorithms and the well-established Analysis, Synthesis,
Evaluation model of the design process. Then, the innovativeness of genetic
algorithms and issues in evaluating and encoding problems are discussed. The
chapter ends by explaining how to represent a problem for a genetic algorithm
using an example from floorplanning in architectural design.
Chapter compares genetic and other search algorithms. It
defines a class of search spaces which are easy for genetic algorithms and hard
for stochastic hill-climbers. Since recombination is the crucial difference
between genetic and other search algorithms, the results provide insight into
the kind of spaces where recombination is necessary. This chapter helps answer
the question of when to expect genetic algorithms to outperform other
algorithms and thus when to use them to greatest effect. An earlier version of
the work reported in this chapter has appeared in [Louis and Rawlins, 1993a].
In chapter the dissertation shows how problem encoding can
bias genetic search. This leads into the important issue of problem encoding
for genetic algorithms in the design domain. A bad encoding can cause a GA to
flounder, to be misled, or both. Modifying the classical genetic algorithm to
mitigate these problems sheds light on the nature of good encodings from the
perspective of genetic algorithms and from the differing perspective of design.
This chapter uses examples from combinational circuit design to illustrate the
results. Parts of this chapter have appeared earlier in [Louis and Rawlins, 1991].
Chapter is concerned with analyzing GA generated designs. The
importance of design analysis lies in being able to explain and subsequently
modify designs in principled ways. Since genetic algorithms are designed for
working in poorly understood spaces, knowledge about the space needs to be
acquired, stored and processed for useful analysis. This chapter shows how to
apply case-based reasoning tools to acquire knowledge about a design space to
explain solutions generated by a GA. Much of this information is implicit in
the processing done by the genetic algorithm. The case-based reasoning tools
extract and process information supplied by the trajectory of a genetic
algorithm through the search space. This organized information in the
case-base can be used to explain how a solution evolved and to help identify
its building blocks. The resulting knowledge base can also be used to tune a
genetic algorithm for that specific domain. Examples from function optimization
and circuit design clarify the results. This work has appeared in
[Louis et al., 1993].
Chapter considers computational complexity, a crucial
element in any computational tool and in any design model where a designer
must specify time limits for a design task. Since evolution is driven by
diversity or variation in a gene pool, the average hamming distance is used
as a diversity metric to derive bounds on the time convergence of genetic
algorithms. Analysis of a flat domain provides worst case time complexity
for static functions. Further, employing linearly computable runtime
information provides tighter bounds on the time beyond which progress is
unlikely on arbitrary static functions. As a by-product, this analysis also
gives qualitative bounds by predicting average fitness, the quality of an
average solution at convergence. Examples from the DeJong test suite of
problems are used to provide supporting empirical evidence. The part of this
chapter on worst case time complexity has appeared in [Louis and Rawlins, 1993b].
The last chapter draws together the threads of representation, analysis, and complexity paving the way toward establishing genetic algorithms as a computational tool for design. Questions and possible avenues of research brought to light by this dissertation are addressed at the end.