There must be a beginning of any great matter, but the continuing unto the end until it be thoroughly finished yields the true glory.Sir Francis Drake.
This thesis' main objective -- to establish genetic algorithms as a computational tool for design -- was achieved by solving four problems considered to be hindering the applicability of genetic algorithms in design. Design was cast as a search through a state space of possible designs, and genetic algorithms were introduced as the search method of choice and contrasted with other applicable search techniques. The mapping between genetic algorithms and the three phase model of design was established. Subsequently, four open problems lying on the path to achieving this objective were identified and overcome. This chapter summarizes the problems and their solutions, discusses results and limitations, and points out areas for future work raised by this dissertation.
Searching in poorly-understood domains is a somewhat unpredictable proposition. There are few guarantees about whether a solution will be found, and if found, what its quality will be. The underlying assumptions made by a search algorithm determine its speed, flexibility, and whether it will in fact find a solution. If an acceptable solution is found, it can be used. However, when a solution is not found, what can the search algorithm's behavior tell us about the search space? This is an important question because 1) any information about a poorly understood space can be made use of in subsequent investigations of the problem and 2) not using available information is, to say the least, wasteful. In design, extracting and using domain information is especially important since sensitivity analysis and post-processing also depend on knowledge gleaned during the course of search. This point of view forms the backdrop for discussing the results in this thesis.
The four problems identified in establishing genetic algorithms as a computational tool for design were:
Once the mapping between genetic algorithms and the three-phase model of
design was established, the question became ``Why should a designer use a
genetic algorithm rather than a hill-climber?'' A related question is ``What
algorithm should a designer use on the problem at hand?''
Chapter 
answered these questions by defining search spaces
in which genetic algorithms perform better, and suggested that such spaces may
be found in design problems formulated as multiobjective or multicriteria
optimization problems. In many cases, such problems involve tradeoffs among
possibly conflicting criteria. Spaces where recombination of two or more
single-criterion optima leads toward a global optimum, with a deceptive basin
in-between to trap hill-climbers, were found to be well suited for genetic
algorithms, especially ones that use pareto optimality in their selection
process (see figure ).
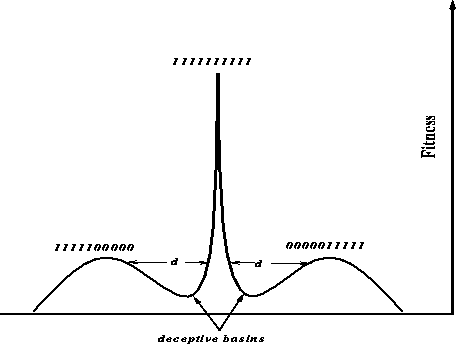
Figure: The type of spaces easy for a genetic algorithm and hard for a
stochastic hill-climber
Pareto-optimal selection maintains the necessary niches until recombination
produces the global optimum. The dissertation defined a problem in hamming
space with these properties (figure ) and empirically compared
performance on the problem for three algorithms:
Pareto-optimal selection also eliminates the need to combine disparate criteria into a single fitness as is usual in genetic algorithms. The method described in this chapter was distributable and computationally less expensive compared to other suggested methods for incorporating pareto optimality [Goldberg, 1989b].
When choosing a search algorithm to attack a particular problem, current
choices include simulated annealing (a stochastic hill-climber) and genetic
algorithms with and without crossover. Most other methods are variations on
these algorithms [Ackley, 1987, Mahfoud and Goldberg, 1992]. Simulated annealing (SA) is a stochastic
hill-climber inspired through an analogy with the cooling of
metals [Kirkpatrick et al., 1983]. It starts with a high temperature T and a
randomly generated initial solution i with a fitness 
. To find a
solution that minimizes F, the SA generates a new solution near i and
accepts this new solution j as the current solution if the fitness of the new
solution, 
, is less than . If is not less than then j
may still be accepted as the current solution with a probability depending on
T. As the temperature decreases during the course of a run, the probability
of accepting j when is not less than decreases. Initially, at
high temperatures almost any change is accepted and the algorithm stresses
exploration over exploitation of the search space. At lower temperatures the
probability of accepting worse solutions is low and the algorithm stresses
exploitation over exploration and converges on a solution.
The differences between a genetic algorithm with no crossover (SHC) and a
simulated annealer are 1) the existence of a cooling schedule (the rate of
decrease of temperature), 2) the fact that simulated annealers are not
population-based, and 3) the convergence behavior, which is usually very
different. Typical convergence behavior for both algorithms on a maximization
problem is shown in figure .
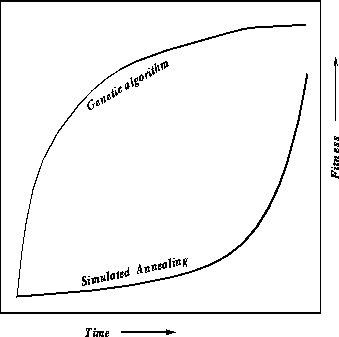
Figure: Comparing convergence behavior of a simulated annealer and a genetic
algorithm
In general, choosing among blind search algorithms is not easy. The assumptions
underlying the algorithms' behavior, the structure of the search space, domain
knowledge, available resources, and personal preference affect this choice. As
shown in chapter , if there are structured local optima
leading towards a global optimum with deceptive basins in between, a genetic
algorithm outperforms other algorithms. Since spaces with such properties may
be found in multicriteria optimization (a large number of design problems are
multicriteria optimization problems), choosing genetic algorithms to attack
these problems makes sense.
The convergence behavior also provides a means of choosing between simulated annealing and genetic algorithms. GAs quickly improve the quality of their solutions, while initially, a simulated annealer only slowly improves quality. Thus, to get a quick solution, a designer may choose a genetic algorithm over a simulated annealer.
Although genetic algorithms outperform stochastic hill-climbers in the kind of spaces described in the chapter, a stronger approach would identify and analyze the properties of a whole range of spaces; from those that are clearly GA- easy and stochastic hill-climbing hard, to spaces that are break-even, where GAs and stochastic hill-climbers are expected to perform similarly. Unimodal spaces clearly confer an advantage to hill-climbers. This thesis identifies one kind of GA-easy spaces, especially relevant to design. A more general theory that includes schema fitness and proportions is an open problem and a matter for further research. Another interesting research problem lies in exploring niche formation with pareto-optimal selection. Stability of niches, cross-breeding among niches, and the role of deception need to be analyzed.
Once a designer has decided to use a genetic algorithm, there comes the task of
encoding a design problem. The biases generated by an encoding and surmounting
unfavorable biases formed the subject of chapter . In
design, epistatic encodings make a GA's preference for schemas of short
defining length a liability. A designer genetic algorithm (DGA) that used a
masked crossover operator to identify and preserve high-fitness schemas of
arbitrary defining length was introduced to alleviate these problems. Elitist
selection was also introduced, both to mesh with masked crossover's properties
and to increase performance. A designer genetic algorithm increased the domain
of application of genetic algorithms by relaxing the emphasis on schemas of
short defining length with an increase in cost of only a constant factor per
generation. Comparing the performance of a classical genetic algorithm and a
designer genetic algorithm also provided information about the space. If the
DGA did better, it meant that highly-fit, low-order schemas were mostly of
large defining length and/or the encoded problem was not deceptive. On the
other hand, if the classical genetic algorithm did better, it meant that the
encoding followed the principle of meaningful building blocks and/or the
problem was partially deceptive. The example used to illustrate these results,
combinational circuit design, was a satisficing problem. The maximum
fitness achievable was known, and the problem was to find a structure that
implemented the specified function.
This chapter illustrated the satisficing nature of some design tasks and provided a tool to mitigate problems in representing designs for genetic algorithms. When designing an encoding, following the principle of meaningful building blocks ensures that epistatic effects are minimized and a genetic algorithm finds smooth sailing. If this principle cannot be followed (lack of domain knowledge, for example), designer genetic algorithms can help. DGAs may solve the problem, or at least provide additional information about the current encoding of the problem. However, designing a good encoding is still something of an art. Masked crossover reduces one encoding problem but there are others that this thesis does not handle. For example, this thesis only considers fixed-length strings and representations that do not produce non-viable offspring. Goldberg's book indicates examples of such problems and how their encodings are handled [Goldberg, 1989b].
Encoding a problem for a genetic algorithm is something of an art. Masked crossover is an option that lowers the aesthetic threshold for genetic algorithm programmers but is more easily misled on deceptive problems. The heuristics used for mask propagation are rather simple, and masks are not evaluated independently of their associated genotypes. This thesis has opted for simplicity and domain independence rather than convergence speed and algorithmic complexity. However, tracking and evaluating mask performance and incorporating any information gleaned from this can lead to better mask rules and finer control of search direction. Structure-synthesis problems in two or three dimensions can also be tackled by developing and using two-dimensional and three-dimensional genotypes and recombination operators. With these representations and operators, schemas of short defining ``area'' or ``volume'' can be preserved without masks by exchanging contiguous areas or convex volumes during crossover. Investigating two-dimensional and three-dimensional genotypes and operators in structure synthesis tasks is an unexplored area with much potential.
The results of chapter illustrated the difficulty of
explaining genetic algorithm generated solutions. Solutions, if found, are
already difficult to understand in poorly-understood domains, using a blind
search algorithm to generate solutions makes understanding such solutions that
much more difficult. Typically, the algorithm is started on a problem, runs
for a preset number of generations/iterations or until some termination
condition is met, and the current best solution or solutions examined. The
examination provides a ranking of current solutions, if there are more than
one, but little else. Why is this solution good? What happens when this
substructure or parameter is changed by a little? Is the response linear or
non-linear? Are there any crucial parts that combined to make this solution
strong? These questions and others are difficult to answer mainly because the
algorithm's trajectory through the search space was not tracked. The sequence
of generated solutions (history) provides information on what the algorithm
considers important in coming up with the current solution set. When combined
with knowledge about a particular algorithm's assumptions about search spaces,
the algorithms history can furnish a designer with information needed to answer
questions about a solution.
The system described in this chapter provides a tool with which designers can explain solutions discovered by genetic algorithms. A module which uses case-based reasoning techniques, is able to organize and make explicit the building blocks used by a GA. Analysis of the building blocks and the path taken by a GA through a search space provides a powerful mechanism for explaining the solutions generated by a GA. Results of the explanation can be used to guide post-processing in order to improve results in case of premature convergence or no convergence. Injecting genetically engineered individuals created through such analysis also improves performance.
As well as providing a system for explaining GA-generated solutions and search-space analysis, the system provides empirical evidence that the building block hypothesis is correct. The hierarchical clustering of a set of GA individuals (distributed over several generations) according to fitness and genotype leads to nested schemas. Analysis shows that the subtrees with the most fit schemas receive the most reproductive energy while the least fit schemas are culled from the population. Although the building block hypothesis implies that clustering on fitness and genotype should yield nested schemas, the system was nonetheless tested on several other clustering possibilities, including more generational information and parental information. Clustering on fitness and genotype was by far the most successful technique. The nested schemas that result from such a clustering provided a coherent index for the case-base.
Chapter made a start at identifying, extracting, organizing, and
storing domain knowledge garnered while searching in a poorly-understood
domain. During the course of future searches, this knowledge can be used and
added to, tuning the algorithm for this particular space. As more and more
knowledge gets added, the search can use this information to increase speed.
The system as a whole gravitates towards the domain dependent (inflexible) but
fast end of the systems spectrum. In other words, this thesis proposes another
use for search methods. Genetic or other blind search algorithms can be used as
explorers of poorly understood domains, with the side effect of inducing a
domain model during the course of search. Initially, in such a system,
there would be little knowledge and much searching. With increasing
knowledge, in subsequent searches, the population of a genetic algorithm would
be seeded with individuals hypothesized to be close to the required solution.
When hypothesized solutions are the required solutions (say more than
50% of the time), the system can be said to have induced a domain model.
Instrumentation for tracking individuals injected by the hypothesis module, a better user interface, and more support for the case-based explanation module need to be added before induction (learning) of domain models can become automated. The work in this thesis only considers case-based systems. Rule-based systems that induce domain models with genetic search already exist and are called classifier systems [Goldberg, 1989b, Holland, 1975].
Last but not least is the problem of computational complexity. In simulated annealing, the annealing schedule defines the number of iterations until termination. In genetic algorithms there was no such upper limit on the time to convergence; in fact, convergence was not well defined. In this chapter, the dissertation advanced a definition of convergence and bounded the time to convergence for genetic algorithms. In addition, using bit complements of population members was identified as a way of maintaining diversity and guarding against deception.
Using the average hamming distance between every pair of individuals in a population (hamming average) as a measure of diversity, a genetic algorithm converges when the change in hamming average is insignificant. Since crossover does not change the hamming average, selection and mutation must be responsible for reducing the hamming average. An upper bound on the time to convergence of a genetic algorithm was therefore provided by a genetic algorithm's performance on a flat function -- that is, a function whose fitness landscape is absolutely flat and all individuals in the GA's population have identical fitness. Mutation rate being fixed, any other function must provide greater selection pressure and thus must converge in a time less than the time taken on a flat function with an identical genotype length. Genetic algorithms converge on the flat function due to genetic drift. This chapter derived an upper bound on the time complexity from considering the effects of drift on allele frequency. Then, from a model of the effect of selection and mutation on the behavior of genetic algorithms, the analysis was able to approximate two solution characteristics at convergence for static search spaces.
In satisficing problems the maximum fitness is known and the structure that attains this fitness needs to be generated. When the maximum fitness is known, the predictability of average fitness at convergence indicates whether the genetic algorithm will succeed, and if so, how long it will take.
The upper limit on time to convergence is an upper limit for all functions of a particular genotypic length. The analysis in this thesis that approximates convergence time by tracking first-order schema proportions assumes low epistatic encodings, and will fail on highly epistatic ones. The other point of view is that epistatic encodings can be detected through this analysis (useful information for a programmer). Finally, since the rate of convergence depends greatly on the selection pressure, it may be possible to tell whether a function is linear, polynomial, or exponential from observing the rate of decrease of hamming average. Finding out broad properties of a space by instrumenting a genetic algorithm can be a very useful area for research.
Design is ubiquitous. Design tasks range from spacecraft design to planning the
day. This thesis helps establish genetic algorithms as a computational tool for
design. Those problems that can be cast as search problems in poorly-understood
domains belong to the set attacked in this thesis. In poorly-understood
domains, genetic algorithms can find solutions to problems in structure
synthesis, structure configuration and parameter instantiation. The thesis
introduced genetic algorithms, compared and contrasted them with other search
algorithms, and explained how to encode problems for GAs. The biases inherent
in genetic search were made explicit and designer genetic algorithms were
defined to help surmount unfavorable biases. Solutions generated in
poorly-understood domains are hard to explain. Using ideas from case-based
reasoning, the system described in chapter tracked, organized,
and stored information during the course of genetic search. This information
was used to explain genetic algorithm solutions and help in sensitivity
analysis. Finally, the time to convergence of a genetic algorithm was bounded.
The thesis settles why, when and how to use genetic algorithms for design, provides tools to explain and analyze genetic algorithm designs, and bounds the time complexity of the task, helping establish genetic algorithms as a computational tool for design.
The work reported here was concerned with laying a firm foundation for exploiting the potential of genetic algorithms in design tasks. However, designer-client interactions usually consist of a cycle of design and modification to design, converging on an acceptable and realizable design. During this cycle the specifications of the design may change, or the tools available to realize the design may change. Modeling these dynamic processes is an open field of research. For example, designing a user interface that over time adapts to a user or group of users is an application area which, with the growth of interest in user interface design, is both interesting and perhaps profitable.
With increasingly powerful computers becoming available, applications in the biological sciences are growing. Genetic algorithms have been used to model aspects of the human immune system [Smith et al., 1993] and for predicting the three-dimensional structure of proteins [Le Grand and Merz Jr., 1993]. The problem of molecular design using computer simulations to provide a measure of the behavior of designed molecules is still open.
Studying complex adaptive systems seeks to understand the underlying commonalities in economies, ecologies, immune systems, and political systems. This field is of particular significance because of the need to predict the effect of changes in our interconnected and interdependent world. Increasing computing power and the availability of accessible electronic data have made the task of simulating and validating complex systems more feasible. Mathematical modeling has often proved inadequate because of the highly non-linear nature of these systems, and direct physical experiments are usually infeasible. Genetic-algorithm-based adaptive systems appear well suited for modeling and controlling complex systems whose aggregate behavior stems from the interaction of constituent parts. For example, one interesting problem is to model the effects of government policy on the state of a resource. The policy's intended effect and its actual implementation after percolating through several layers of society are difficult to reconcile. Modeling such a complex system is a first step toward effective policy making. A genetic-algorithm-based classifier system using feedback on the state of the resource may be able to learn effective strategies to manage the resource optimally.
The number of possible applications is growing. With continued growth in the speed and size of computer systems, larger and more complex problems will be amenable to genetic search. The work reported in this dissertation will hopefully help lay the foundations for the growth of genetic algorithms in design.