|









| |
        |
|
Imposing
rigidity constraints to the predicted views |
|
To recognize the novel views of an object, the idea is to use algebraic
functions of views to predict all the views that a group of model
points can produce and represent it the predictions in some index structure.
As a result, each parameter's range is actually sampled into a finite number
of points and a finite number of transformed model groups is generated only.
Because using two reference views is only applicable to general linear
transformations of the object, without additional constraints, it is
impossible to distinguish between rigid and linear but not rigid
transformations of the object. To impose rigidity (with possible scaling),
the coefficients must meet two constraints: |
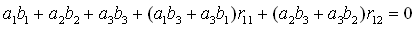 (1)
(1) |
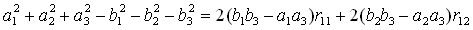 (2) (2) |
|
where (a1, a2, a3, b1,
b2, b3) are the parameters of the algebraic functions,
r11, and r12 are the first two elements of the first
row in the rotation matrix of the second view. These two constraints
satisfies under the condition that the rotation matrix of the first
reference view must be identity matrix. Therefore, to meet these two
constraints, we have to select the two reference views in the specific way:
(1) the rotation matrix of the two views are known; (2) the rotation matrix
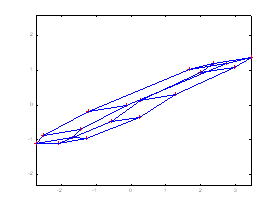
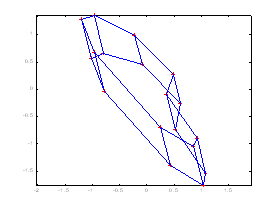
of the first reference view is identity matrix. Figure 1 shows two different
generated views of the car model without and with imposing the rigidity
constraints respectively. With imposing the rigidity constraints, the
unrealistic views like (a) can be discarded. |
|
 |
 |
|
Figure 1. (a) Unrealistic view generated without
imposing the rigidity constraints (b) Realistic view generated with
imposing the rigidity constraints |
|
Back
to Top |
|
![]()