|








| |
        |
|
Background of Algebraic Functions of Views |
| Given an object undergoing 3d rigid
transformations, assume the images of the object are obtained by orthographic
projection followed by a uniform scaling, the novel view of the object can be
expressed as a linear combination of three other views of the same
object. Given
3 reference views of the same object, V1, V2, V3,
under different rigid transformations, three points
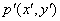 in V1, in V1,
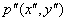 in V2, in V2,
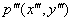 in V3 are
in correspondence, the correspondence points p(x,y) in the novel view V can be
expressed as in V3 are
in correspondence, the correspondence points p(x,y) in the novel view V can be
expressed as
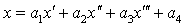
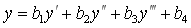 (1)
(1)
For general linear transformations, it is possible to use instead just two
reference views of the objects:
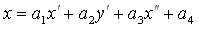
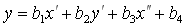 (2)
(2)
where aj, bj, j=1,...,4, are the same for all the
points which are in correspondence across the three views. Figure 1 shows an
example of object model and its linear combinations.
|
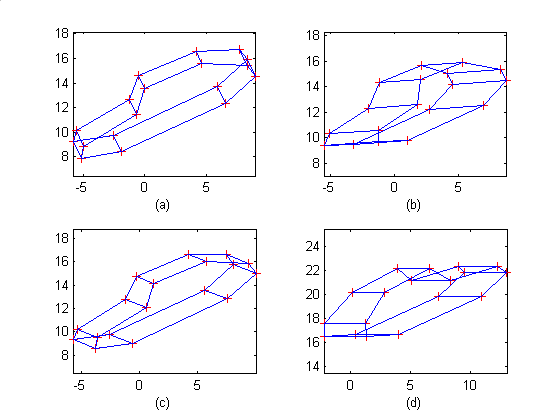 |
| Figure
1. (a) and (b) are two reference views of a CAD car
model. Figure (c) and (d) are two generated novel views of based on Equation
(2). The coefficients for (c) are [0.6940, 0.0280, 0.3660, 0.0903] for x,
and [-0.1427, 1.0131,0.1707, 0.0421] for y. The coefficients for (d) are
[-1.1103 -0.6058 0.8112 13.0479] for x, and [-0.9840 0.7175, 0.3782,
11.5897] for y. |
| Back to Top |
|
![]()