        |
|
Although AFoVs allow us to generate the views that an
object can produce efficiently, representing this information compactly
would be critical. We have decided to use statistical learning techniques
for this purpose. In particular, the views that an object can produce form
a manifold in a lower-dimensional space. This manifold can be learned
efficiently using Gaussian mixture models and the EM (Expectation
Maximization) algorithm. The main advantage in our case is that we can
generate a large number of sampled views using AFoVs, therefore, improving
our chances to reveal and learn the true structure of the manifold. |
|
Mixture models are a type of density model which
comprises a number of component functions, usually Gaussian. These
component functions are combined to provide a multimodal density. Once a
model is generated, posterior probabilities can be computed according to
the Bayes' rule. A mixture is defined as a weighted sum of K components
where each component is a parametric density function |
|
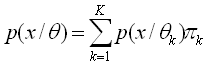
|
|
Each mixture component is a Gaussian function: |
|
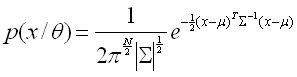
|
|
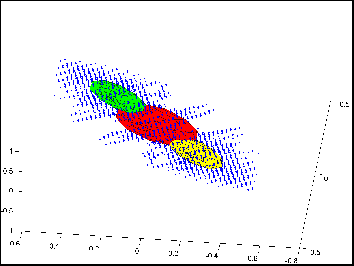
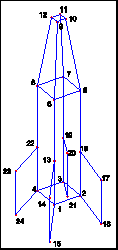
Figure1 shows the manifold obtained for a group of 8
points from an artificial object used in our experiments. |
|
|
|
|
(a) |
(b) |
|
Figure 1 The mixture model obtained (shown in (a) for a
group of 8 point features) from artificial object shown in (b). |
|
Each hypothesis generated by the k-d tree search is
ranked by computing its probability using the learned manifolds described
above. Specifically, for each test view, we compute two probabilities, one
from the x-coordinates of the view and the other from the y-coordinates of
the view. The overall probability is then computed as follows: |
|
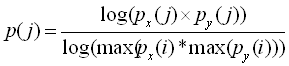
|
|
Back to Top |
![]()