|









| |
        |
|
Estimating the ranges of
values for the parameters in the algebraic functions |
|
Given the
point correspondence across the three views, the following system of
equations must be satisfied: |
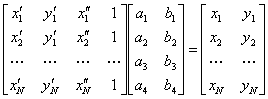
|
(1) |
where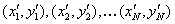 and and
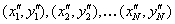 are the coordinates of the
points of the reference views V1 and V2,
respectively, and are the coordinates of the
points of the reference views V1 and V2,
respectively, and 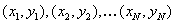 are the coordinates
of points of the novel view V. Splitting the above system of equations
into two subsystems, one involving the aj parameters and
one involving the bj parameters, we have are the coordinates
of points of the novel view V. Splitting the above system of equations
into two subsystems, one involving the aj parameters and
one involving the bj parameters, we have |
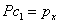
|
(2) |
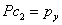
|
(3) |
|
where P is the matrix formed by x and y coordinates of
the reference views (plus a column of 1's), c1 and c2
are vectors corresponding to aj 's and bj's
(the parameters of the algebraic functions), and px and
py are vectors corresponding to the x and y coordinates
of the novel views. Both (2) and (3) are overdetermined which means that
they can be solved using least squares approach such as SVD. By SVD, |
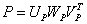
|
(4) |
|
The solutions of the above two systems are |
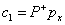
|
(5) |
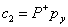
|
(6) |
where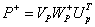 is the
pseudoinverse of P. In specific, the solution of (2) and (3) are given by is the
pseudoinverse of P. In specific, the solution of (2) and (3) are given by |
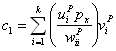
|
(7) |
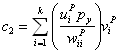
|
(8) |
where
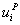 denotes the ith
column of matrix UP, denotes the ith
column of matrix UP,
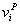 denotes the ith
column of matrix Vp, and k=4. To determine the range of
values for c1 and c2, we assume that the novel views
has been scaled such that the x and y coordinates belong within a specific
interval. This can be done, for example, by mapping the novel view
to the unit square [0,1]. Applying the interval arithmetic operators to
(7) and (8), we can compute interval solutions for c1 and c2
by setting px=[0,1] and py=[0,1]. To
make it clear, the ith component of c1, i=1,...,
k, can be rewritten as: denotes the ith
column of matrix Vp, and k=4. To determine the range of
values for c1 and c2, we assume that the novel views
has been scaled such that the x and y coordinates belong within a specific
interval. This can be done, for example, by mapping the novel view
to the unit square [0,1]. Applying the interval arithmetic operators to
(7) and (8), we can compute interval solutions for c1 and c2
by setting px=[0,1] and py=[0,1]. To
make it clear, the ith component of c1, i=1,...,
k, can be rewritten as: |
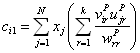
|
(9) |
The interval solution
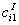 can now be obtained by applying the interval arithmetic operations on the
equation above. Similarly, we can obtain the interval solutions for the
rest elements of
can now be obtained by applying the interval arithmetic operations on the
equation above. Similarly, we can obtain the interval solutions for the
rest elements of 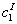 as
well as as
well as 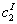 . It should be
noted that both (7) and (8) involve the same matrix P and px
and py assume values from the same interval, the
interval solution . It should be
noted that both (7) and (8) involve the same matrix P and px
and py assume values from the same interval, the
interval solution 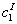 and and
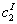 will be the same. will be the same. |
|
Back
to Top |
|
![]()